Author: Ronen Shekel
Imagine a box with two balls: one red, one blue. Alice takes one ball to Mars and Bob takes the other to Andromeda. The moment Alice opens her box and sees a blue ball: she instantly knows Bob’s is red. This might seem like what Einstein called “spooky action at a distance” [1], but it is not entanglement. This is classical correlation. The properties were fixed from the start.
The Quantum Hallmark: Correlations in Multiple Bases
A hallmark of quantum entanglement is the existence of strong correlations in multiple, incompatible measurement bases [2].
Consider a Bell state, a state in a coherent superposition of horizontal and vertical polarizations, |HH>+|VV>. If Alice and Bob both agree to measure in the H/V basis (for example, by setting their polarizers to 0°/90°), they will find perfect correlations: if Alice gets H, Bob gets H. If she gets V, he gets V. So far, this is just like the red and blue balls.
But if they both agree to switch to an incompatible basis, like the basis of diagonal (D) and anti-diagonal (A) polarization, their results will still be perfectly correlated. This is unique to coherent quantum correlations.
Now, compare this to a simple, non-entangled state, like |HH>. In the H/V basis, their results are perfectly correlated. But if they both measure in the D/A basis, the correlations vanish. The results are random; if Alice measures D, she has no idea if Bob will get D or A.
Bell inequalities are tests designed to measure these very correlations across multiple bases [3, 4]. Rigorous certification of entanglement by violating these inequalities is essential for quantum technologies, from quantum computing to secure communication.
Certifying High-Dimensional Entanglement with SFG
This concept isn’t limited to two-dimensional polarization. As we’ve discussed in a previous post on spatial entanglement, entanglement can be high-dimensional, existing in the spatial properties of photons, where two mutually unbiased bases could be for instance the near-field and far-field distributions. Entanglement could also manifest in the time-energy properties of photon pairs.
In Spontaneous Parametric Down-Conversion (SPDC), a narrowband pump photon splits into two twin photons. Due to energy conservation, the sum of their frequencies ν₁ + ν₂ is precisely fixed. And because they are born at the same instant, the time difference between them (t₁ − t₂) is incredibly small.
For any separable, classical-like state, the uncertainties in these correlated quantities obey a fundamental bound: Δ(t₁ − t₂)Δ(ν₁ + ν₂) ≥ 1⁄2 [5]. A quantum-entangled pair, however, can violate this.
To prove this violation, we cannot simply measure the individual times and frequencies of each photon separately, since doing so would destroy the joint correlation information we seek to certify. Instead, we must perform a global measurement that probes the combined variables (t₁ − t₂) and (ν₁ + ν₂) directly, without accessing the individual values.
Sum-Frequency Generation (SFG) is an ideal tool for this. As the reverse of SPDC (Fig. 1), SFG requires both photons to arrive simultaneously at the crystal, effectively acting as an ultrafast coincidence detector for t₁ − t₂ ≈ 0. Furthermore, it annihilates both photons to create one new photon whose frequency is the sum ν₁ + ν₂, which can then be measured precisely.
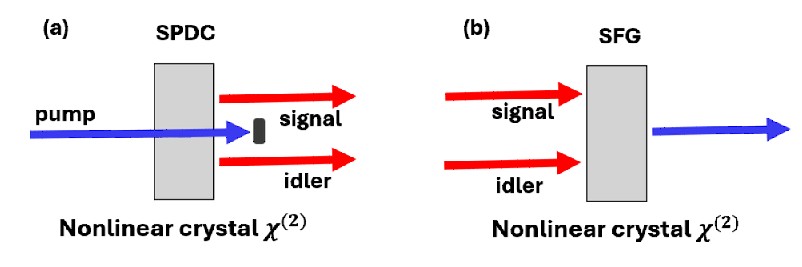
While this idea has been known for years [6, 7], direct SFG with single photons is notoriously inefficient. Recently [8], a groundbreaking experiment from Prof. Avi Pe’er’s group at Bar-Ilan University shattered this barrier, violating the classical bound by an astonishing 12 orders of magnitude. Using a high-quality PPKTP crystal to generate biphotons with an extreme bandwidth of 113 THz, they employed Coherent SFG, where a strong pump stimulates the recombination, to efficiently and directly measure the joint correlation.
The Crystal Connection
The success of such record-breaking work relies on the exceptional quality of nonlinear crystals. At Raicol we are proud to provide such high-quality crystals and are happy to contribute to research pushing the boundaries of quantum science. We are also active participants in international collaborations, such as the European QuantERA project SPARQL, dedicated to advancing quantum technologies.
Time-energy entanglement arises naturally and intrinsically in SPDC through energy conservation – it requires no additional engineering. But how can we engineer entanglement in the polarization degree of freedom? Stay tuned for our next post.
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
References
[1] Einstein, A., & Born, M. (1971). Letter from Einstein to Max Born, 3 March 1947. In B. M. Walker (Ed.), The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955 (pp. 157-158). New York.
[2] Giese, Enno. “Entanglement and Its Verification: A Tutorial on Classical and Quantum Correlations.” arXiv preprint arXiv:2511.09507 (2025).
[3] Bell, John S. “On the einstein podolsky rosen paradox.” Physics Physique Fizika 1, no. 3 (1964): 195.
[4] Clauser, John F., Michael A. Horne, Abner Shimony, and Richard A. Holt. “Proposed experiment to test local hidden-variable theories.” Physical review letters 23, no. 15 (1969): 880.
[5] Mei, Yefeng, Yiru Zhou, Shanchao Zhang, Jianfeng Li, Kaiyu Liao, Hui Yan, Shi-Liang Zhu, and Shengwang Du. “Einstein-podolsky-rosen energy-time entanglement of narrow-band biphotons.” Physical Review Letters 124, no. 1 (2020): 010509.
[6] Dayan, Barak, Avi Pe’er, Asher A. Friesem, and Yaron Silberberg. “Nonlinear interactions with an ultrahigh flux of broadband entangled photons.” Physical review letters 94, no. 4 (2005): 043602.
[7] MacLean, Jean-Philippe W., John M. Donohue, and Kevin J. Resch. “Direct characterization of ultrafast energy-time entangled photon pairs.” Physical review letters 120, no. 5 (2018): 053601.
[8] Nechushtan, Nir, Hanzhong Zhang, Yosef London, Mallachi Meller, Haia Amichai, Eliahu Cohen, and Avi Pe’er. “Quantum matched filtering: breaking time-energy separability by 12 orders of magnitude.” arXiv preprint arXiv:2503.03583 (2025).
