Author: Ronen Shekel
One of the most remarkable features of quantum theory is entanglement, where quantum systems show nonlocal correlations between particles or photons that are impossible to explain using classical physics. This can famously be demonstrated, for example, by violating a Bell inequality [1, 2]. While in many cases entanglement between two-level systems (qubits) is discussed, high-dimensional entanglement between multi-level systems provides an even richer structure.
High-dimensional entangled states are attractive because they have a greater information capacity, and also show increased resistance to noise and losses [3]. Additionally, it is relatively straightforward to generate high-dimensional entangled states using spontaneous parametric down-conversion (SPDC), and to shape them using liquid crystal spatial light modulators [4].
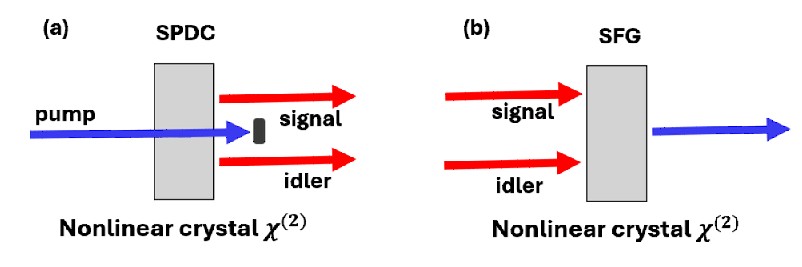
In SPDC [5], a strong plane-wave pump beam impinges upon a nonlinear crystal such as PPKTP (Periodic polled KTP). With some probability, related to the crystal’s nonlinear coefficients, a pump photon will be annihilated, and two entangled photons will be created (Fig. 1a). Since energy must be conserved, the frequencies of these two photons must sum to that of the pump photon, and here we will assume the degenerate case, where they have the same frequency (Fig. 1b). Since momentum must be conserved, the wave vectors of the created photons must add up to that of the pump photon, which is pointing in a specific direction, since the pump is a plane wave. Consequently, the two photons will have anti-correlations in their transverse momentum (Fig. 1c). This means that if one photon is emitted with a certain angle, its twin will be emitted in the opposite direction with respect to the pump beam.
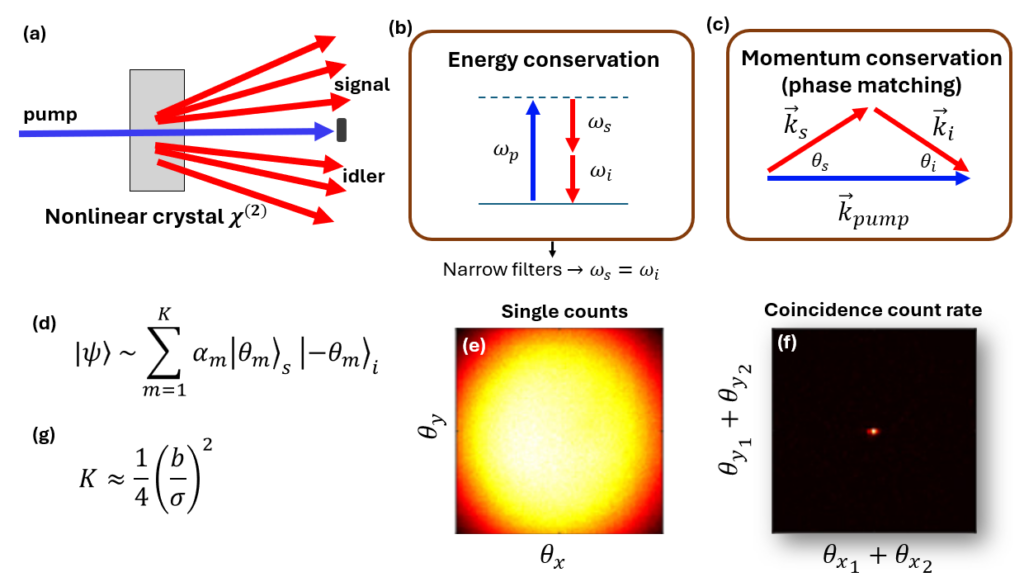
In fact, the generated state of these two photons is a coherent superposition of emission in these different angles, each photon in an opposite direction, with coefficients that depend on the exact phase-matching conditions (Fig. 1d), and typically depend on the angles like a sinc function [5]. These correlations may be measured in the far-field. Using a simple camera, we observe the “single counts”, which is the average intensity of photons emitted in all the directions permitted by the phase matching, which may be a rather wide region (Fig. 1e). Performing coincidence measurements, however, will reveal that given that one photon was measured in a certain angle, the twin photon will always be strongly correlated, and will be found in a much smaller “coincidence region” (Fig. 1f).
The ratio between the coincidence region and the single counts region quantifies the number of distinct modes in the quantum superposition, which is related to its Schmidt rank [6, 7] (Fig. 1g). Hence, to tailor the spatial entanglement properties in SPDC, one should consider both the width of the phase matching function (controlling the single counts region) and the strength of the correlations, and plan an optical setup accordingly.
Specifically, the angular width b of the phase matching sinc function, or equivalently, the angular range allowed by the SPDC process, is determined by the pump wavelength λ_p, and by the crystal thickness L, and is approximately. √(λ_p/L) Thus, while using a thin crystal will result in smaller SPDC flux due to a shorter interaction length, it will typically allow a larger range of emission angles, and will generate highly spatially entangled states.
Conversely, the width of the coincidence region is determined by the angular spectrum of the pump, σ. Indeed, for a plane-wave pump with a single well-defined momentum vector, we expect perfect correlations. However, a finite pump beam will necessarily contain many different angles, which will allow an angle mismatch in the momentum conservation. This is referred to more generally as the transfer of angular spectrum from the pump to the SPDC correlations [8].
In conclusion, having a wide pump beam with a narrow angular spectrum, and using a thin crystal, will increase the dimensionality of the SPDC spatial entanglement. The same reasoning about the number of effective modes can equivalently be carried out in the near-field: A wide pump beam yields a correspondingly large emission area of the SPDC photons, and a thin crystal results in each pair of photons being strongly spatially correlated at the output of the crystal due to the small propagation distance traveled from their point of generation [6, 9].
Of course, one doesn’t always want high-dimensional spatial entanglement. For instance, in many cases, SPDC photons are coupled into single-mode fibers. In such a case, we would like to generate only a single spatial mode to get good coupling to the fiber. A good rule of thumb for this is to set the Rayleigh length of the pump to be the length of the crystal.
At Raicol, we provide a variety of nonlinear crystals with a rich range of parameters, allowing you to design your optical setup exactly for your needs. We also provide custom-made periodic polled crystals with specially tailored polling, allowing the shaping of the two-photon joint spectral intensity [10], which will be the subject of a different post. For more information, please visit our products page, and contact us if you have any questions.
[1] Bell, John S. “On the einstein podolsky rosen paradox.” Physics Physique Fizika 1, no. 3 (1964): 195.
[2] Brunner, Nicolas, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. “Bell nonlocality.” Reviews of modern physics 86, no. 2 (2014): 419.
[3] Ecker, Sebastian, Frédéric Bouchard, Lukas Bulla, Florian Brandt, Oskar Kohout, Fabian Steinlechner, Robert Fickler et al. “Overcoming noise in entanglement distribution.” Physical Review X 9, no. 4 (2019): 041042.
[4] Defienne, Hugo, Matthew Reichert, and Jason W. Fleischer. “Adaptive quantum optics with spatially entangled photon pairs.” Physical review letters 121, no. 23 (2018): 233601.
[5] Walborn, Stephen P., C. H. Monken, S. Pádua, and PH Souto Ribeiro. “Spatial correlations in parametric down-conversion.” Physics Reports 495, no. 4-5 (2010): 87-139.
[6] Lib, Ohad. “Utilizing the Spatial Degree of Freedom of Entangled Photons for High-Dimensional Quantum Information Processing”, PhD thesis.
[7] Law, C. K., and J. H. Eberly. “Analysis and interpretation of high transverse entanglement in optical parametric down conversion.” Physical review letters 92, no. 12 (2004): 127903.
[8] Monken, Carlos Henrique, PH Souto Ribeiro, and Sebastiao Pádua. “Transfer of angular spectrum and image formation in spontaneous parametric down-conversion.” Physical Review A 57, no. 4 (1998): 3123.
[9] Schneeloch, James, and John C. Howell. “Introduction to the transverse spatial correlations in spontaneous parametric down-conversion through the biphoton birth zone.” Journal of Optics 18, no. 5 (2016): 053501.
[10] Shukhin, Anatoly, Inbar Hurvitz, Sivan Trajtenberg-Mills, Ady Arie, and Hagai Eisenberg. “Two-dimensional control of a biphoton joint spectrum.” Optics Express 32, no. 6 (2024): 10158-10174.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.