Author: Dr. Noa Voloch Bloch and Ori Levin
Raicol, a renowned leader in PPKTP manufacturing, is committed to propelling the quantum industry forward through state-of-the-art solutions. Over the past few years, our relentless pursuit of excellence has led to significant enhancements in our manufacturing capabilities. Notably, we have dedicated substantial efforts to refining our proficiency in producing shorter poling periods.
While achieving short poling periods for individual elements with low yields is indeed feasible, the real challenge lies in scaling this capability for mass production and making it accessible to our valued customers at a competitive price point. Our engineer, Mr. Michael Schindler, has achieved a breakthrough by developing a process that enables extremely short poling periods (a full cycle of approximately 1 µm). As a result, we are proud to offer a standard poling period of less than 3 µm.
At Raicol, we remain committed to pushing the boundaries of what’s possible in the quantum industry, and our dedication to innovation continues to drive our success.
Narrow bandwidth SPDC
Raicol recently experienced a significant increase in demand for PPKTP crystals with extremely short poling periods. This demand was primarily driven by applications in narrow-band “Counter Propagation SPDC,” which can achieve bandwidths as low as 0.06 nm [1,2]. The importance of these narrow bandwidths lies in their potential for integrating SPDC sources with quantum memories, where matching the bandwidths of atomic transitions and exciting radiation is crucial. The relationship between crystal length and SPDC bandwidth is inverse, with longer crystals producing narrower bandwidths. While Raicol continues to improve its capabilities in this area, the company currently offers PPKTP crystals up to 30 mm in length. This development demonstrates Raicol’s ongoing commitment to advancing quantum technologies and meeting the evolving needs of the photonics industry. As the field of quantum optics continues to progress, Raicol remains dedicated to exploring innovative solutions and pushing the boundaries of PPKTP crystal manufacturing. The company’s efforts in producing crystals with extremely short poling periods and longer lengths are contributing to the advancement of quantum memory integration and other cutting-edge applications in quantum technologies.
Production validation to short poling
As a leader in nonlinear crystal manufacturing we maintain rigorous quality control procedures, especially when developing new crystals or cutting-edge technologies. When trying to implement short poling we faced challenge in characterizing and validating short-polled KTP crystals. While Raicol’s measuring testing systems are typically designed for forward-propagating Second Harmonic Generation (SHG) and Spontaneous Parametric Down-Conversion (SPDC) across various wavelengths. However, the short-period polled KTP crystals presented a distinct obstacle. The absence of forward SHG/SPDC processes corresponding to the short period, due to their occurrence near the edge of the KTP transmission window, made conventional collinear second harmonic processes unsuitable for evaluation of 1.2 µm polled crystals. This situation underscores the complexity of validating advanced crystal technologies and highlights Raicol’s commitment to ensuring product performance through innovative testing methodologies.
A. Backward second harmonic generation
There are two distinct types of collinear second harmonic generation SHG processes [3]: forward and backward propagation:
Forward Second Harmonic Generation: In this process, the beam at the doubled frequency propagates in the same direction as the beam at the fundamental frequency. In the case of PPKTP the shortest poling period enabling efficient frequency doubling from 800 nm pump to 400 nm is approximately 3 µm.
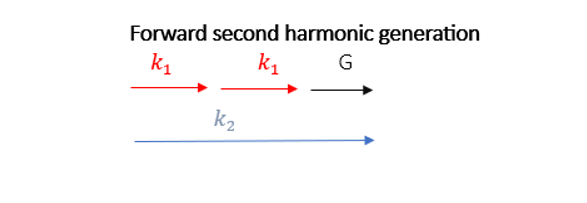
Backward Second Harmonic Generation: In this process, the generated wave propagates in the opposite direction of the pump.
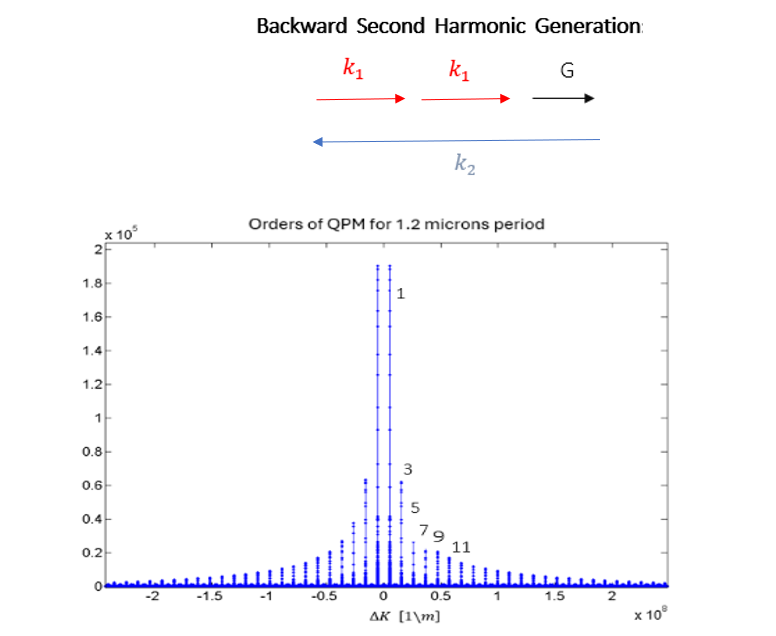
However, the periods necessary for efficient backward second harmonic generation for visible wavelengths are extremely short and pose significant manufacturing challenges. For example, generating a second harmonic of 829 nm light in the first-order QPM requires a period of 0.109 µm.
B. Backward propagation test bench
In order to characterize our 1.2 short poling crystals we measure SH backward propagation, we evaluated the ΔK that matches the phase matching values of 1.2 µm grating periods. For the ΔK values shown in the graph there is no forward process. But for the 829 nm converted to 414.4 nm at 33 deg PPKTP
The ΔK is 5.754⋅10^7 [1/m] specifically suites phase matching of the 11-th order shown in the graph. Backward second harmonic generation of 829 nm converted to 414.5nm [3].
To overcome this challenge, we implement a backward propagation test system, as outlined below: The 829 nm pump beam enters the crystal and the SH which propagates backward is deflected by a dichroic mirror to the detector.

[1] Liu, YC., Guo, DJ., Ren, KQ. et al. Observation of frequency-uncorrelated photon pairs generated by counter-propagating spontaneous parametric down-conversion. Sci Rep 11, 12628 (2021).
[2] Zhang, H., Jin, XM., Yang, J. et al. Preparation and storage of frequency-uncorrelated entangled photons from cavity-enhanced spontaneous parametric downconversion. Nature Photon 5, 628–632 (2011).
[3] S. Moscovich, A. Arie, R. Urenski, A. Agronin, G. Rosenman and T. Rosenwaks, “Noncollinear second harmonic generation in sub-micrometer poled RbTiOPO4”, Optics Express, 12, 2236-2242 (2004).
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
Quantum and classical ghost imaging
Ghost imaging, one of the first imaging techniques using quantum light, has captivated researchers since its inception in the mid-1990s. The concept of ghost imaging was first demonstrated in 1995 by Pittman et al. [1], using quantum light generated via spontaneous parametric down-conversion (SPDC), a nonlinear optical process that converts a pump photon into two lower-energy entangled photons.
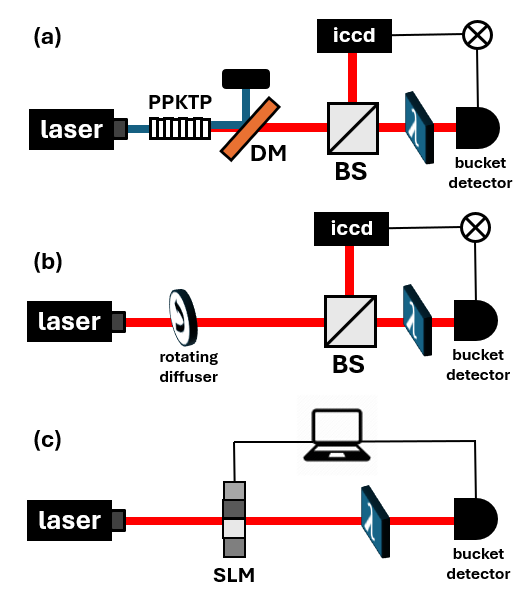
In this experiment (Fig. 1a), the spatially entangled photons are separated, with one photon propagating through an object and being collected using a bucket detector with no spatial resolution, while the idler photon is sent to a multi-pixeled camera. By measuring coincidence events between the bucket detector and the camera, the object is reconstructed, despite the fact that the photons detected by the camera did not directly interact with it! This nonlocal characteristic led to the term “ghost imaging.”
The crux of this technique lies in the spatial correlations of the two photons: areas that are blocked by the object will not reach the bucket detector, so coincidence events will not occur with the corresponding pixels in the camera. But one must remember: correlations do not necessarily imply entanglement! Does quantum entanglement play a critical role in this technique? This was the subject of a debate that lasted several years.
In [2], for instance, theoretical arguments were presented, suggesting that entanglement is intrinsic to ghost imaging. However, in 2002, Bennik et al. [3] demonstrated ghost imaging using two classically correlated beams, randomly deflected at different angles. Others explored similar classical correlations using a rotating diffuser [4], generating correlated pseudo-thermal light (Fig. 1b).
Computational ghost imaging
An important fruit of this debate was that of computational ghost imaging, proposed by Shapiro [5], and demonstrated by Bromberg et al. [6]. In this method, only a single detector is used, and the high-resolution camera is replaced by a computation of the propagating field which is shaped using a spatial light modulator (Fig. 1c). The key point here is that we know everything about the photon propagating to the camera, so we can utilize this knowledge computationally and get rid of the physical camera. The object image is obtained by correlating the intensities measured by the bucket detector with the calculated field at the object plane.
While this computational approach already simplified the experimental setup, researchers soon realized [7] that the number of measurements could be significantly reduced by leveraging modern image processing techniques, particularly those that exploit prior knowledge about the image structure. Remarkably, for most imaging tasks, such information exists: natural images are sparse, that is, they contain many coefficients close to or equal to zero when represented in an appropriate basis. This property of natural images is at the core of modern lossy image compression algorithms, such as JPEG. The field of compressed sensing exploits this sparsity/compressibility to reduce the number of measurements needed for faithful image recovery. Utilizing this technique reduces the number of measurements required for a faithful reconstruction by an order of magnitude.
Current state and future directions
The fact that computational ghost imaging uses only a single detector provides experimental evidence that pseudothermal ghost imaging does not inherently rely on nonlocal quantum correlations. It is now also recognized that the quantum and classical methods produce images of a similar resolution. The main advantage of utilizing quantum light for ghost imaging is found at low light levels, at which the quantum modality exhibits greater visibility and a greater signal-to-noise ratio [8]. This could be especially important when imaging samples that are sensitive to high light levels. Further details comparing the classical and quantum modalities may be found in [9].
Almost 30 years since its first demonstration, many extensions, applications, and modalities of ghost imaging are still being explored. Are you interested in ghost imaging with quantum light? Or perhaps want to explore other use cases for quantum entanglement? Please check out our PPKTP crystal and BBO crystals, used for generating entangled photons, and join the conversation!
[1] Pittman, Todd B., Y. H. Shih, D. V. Strekalov, and Alexander V. Sergienko. “Optical imaging by means of two-photon quantum entanglement.” Physical Review A 52, no. 5 (1995): R3429.
[2] Abouraddy, Ayman F., Bahaa EA Saleh, Alexander V. Sergienko, and Malvin C. Teich. “Role of entanglement in two-photon imaging.” Physical review letters 87, no. 12 (2001): 123602.
[3] Bennink, Ryan S., Sean J. Bentley, and Robert W. Boyd. ““Two-photon” coincidence imaging with a classical source.” Physical review letters 89, no. 11 (2002): 113601.
[4] Valencia, Alejandra, Giuliano Scarcelli, Milena D’Angelo, and Yanhua Shih. “Two-photon imaging with thermal light.” Physical review letters 94, no. 6 (2005): 063601.
[5] Shapiro, Jeffrey H. “Computational ghost imaging.” Physical Review A—Atomic, Molecular, and Optical Physics 78, no. 6 (2008): 061802.
[6] Bromberg, Yaron, Ori Katz, and Yaron Silberberg. “Ghost imaging with a single detector.” Physical Review A—Atomic, Molecular, and Optical Physics 79, no. 5 (2009): 053840.
[7] Katz, Ori, Yaron Bromberg, and Yaron Silberberg. “Compressive ghost imaging.” Applied Physics Letters 95, no. 13 (2009).
[8] Moreau, Paul-Antoine, Ermes Toninelli, Thomas Gregory, and Miles J. Padgett. “Imaging with quantum states of light.” Nature Reviews Physics 1, no. 6 (2019): 367-380.
[9] Erkmen, Baris I., and Jeffrey H. Shapiro. “Ghost imaging: from quantum to classical to computational.” Advances in Optics and Photonics 2, no. 4 (2010): 405-450.
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
One of the most beautiful experiments with SPDC light is that of induced coherence. It has originally been demonstrated and analyzed by Zou, Wang, and Mandel in 1991 [1, 2], and is discussed and utilized to this day. In this experiment two nonlinear crystals are used, set in a configuration as shown in Fig. 1.
A “green” pump beam generates via parametric down conversion “yellow” signal and “red” idler photons, both in the first crystal and in the second crystal. We then slightly change the length difference between the paths of the two yellow signal photons and measure their interference using a single photon detector (D1). The question arises – will we measure interference fringes? Are these signals coherent with each other?
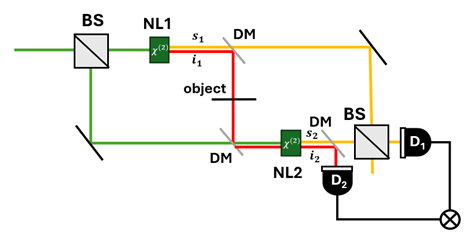
Well, since we cannot know which of the two signal photons we are measuring, we should indeed sum the amplitudes, and do observe interference. However, consider now a case where we block the path of the first idler photon (). Remarkably, even though signal photons can still originate from either the first or the second crystal, the fringes will disappear!
This may again be explained in terms of distinguishability. In Feynman’s words [3]:
If you cannot distinguish the final states even in principle, then the probability amplitudes must be summed.
Further examination of our system shows that blocking the first idler photon does affect the distinguishability between the two signal photons. If the signal photon is accompanied by an idler photon at the second detector (D2) then we know that it originates from the second crystal. If we don’t measure an idler photon – we know that it has been blocked, and that the signal photon originates from the first crystal. Thus, blocking the first idler photon reduces the indistinguishability between the two signal photons.
This is quite remarkable. Even when both processes have a low flux, and statistically, in no point in time the first idler and the second signal photon co-exist, the mere theoretical possibility of measuring the idler photon from the first crystal affects the coherence properties of the signal photon generated in the second crystal. For this reason, we say that the idler photon induces the coherence of the process.
In 2014, this effect has been utilized in the group of Nobel prize winner Anton Zeilinger, in the context of imaging [4]. Consider that we block only part of the path of this idler photon and swap the single photon detector with a sensitive camera. The area on the camera corresponding to the blocked area will show no interference, while the other area will show interference.
Measuring intensity that depends on the transmittance of an object is of course exactly what we want to do in imaging! Notice however the puzzling fact: the light measured by the camera never passed through the object, and the light hitting the object never reaches the camera!
A second modality for using induced coherence for imaging is for phase imaging: the phase accumulated by the idler photon is simply transferred to the signal photon. Such a modality provides interesting configurations such as where the light hitting the object is at a wavelength not detectable by the used camera. Alternatively, it also works when the object is completely transparent or even completely opaque in the wavelength detected by the camera.
While this imaging technique is no doubt intriguing, providing materials for many new experiments conducted to this day [5], the exact quantum nature of the method has been debated. Indeed, in [6] it has shown that virtually all the features of the experiment can be realized in a quantum-mimetic fashion using classical light. The discussion has since continued, for example in [7] and [8].
In various undetected photon experiments different nonlinear crystals have been used, such as BBO or PPKTP, but in principle almost any nonlinear process could produce similar results [4]. If you want to join the discussion, get your own crystals at Raicol, where we provide the best world-class nonlinear crystals and find your own novel imaging modality!
[1] Zou, X. Y., Lei J. Wang, and Leonard Mandel. “Induced coherence and indistinguishability in optical interference.” Physical review letters 67, no. 3 (1991): 318.
[2] Wang, L. J., X. Y. Zou, and L. Mandel. “Induced coherence without induced emission.” Physical Review A 44, no. 7 (1991): 4614.
[3] Feynman, Richard P. (Richard Phillips), 1918-1988. The Feynman Lectures on Physics. Reading, Mass. :Addison-Wesley Pub. Co., 19631965. Vol. III, chapter 03, “Probability Amplitudes”.
[4] Lemos, Gabriela Barreto, Victoria Borish, Garrett D. Cole, Sven Ramelow, Radek Lapkiewicz, and Anton Zeilinger. “Quantum imaging with undetected photons.” Nature 512, no. 7515 (2014): 409-412.
[5] Pearce, Emma, Osian Wolley, Simon P. Mekhail, Thomas Gregory, Nathan R. Gemmell, Rupert F. Oulton, Alex S. Clark, Chris C. Phillips, and Miles J. Padgett. “Single-frame transmission and phase imaging using off-axis holography with undetected photons.” arXiv preprint arXiv:2403.13389 (2024).
[6] Shapiro, Jeffrey H., Dheera Venkatraman, and Franco NC Wong. “Classical imaging with undetected photons.” Scientific Reports 5, no. 1 (2015): 10329.
[7] Kolobov, Mikhail I., Enno Giese, Samuel Lemieux, Robert Fickler, and Robert W. Boyd. “Controlling induced coherence for quantum imaging.” Journal of Optics 19, no. 5 (2017): 054003.
[8] Lahiri, Mayukh, Armin Hochrainer, Radek Lapkiewicz, Gabriela Barreto Lemos, and Anton Zeilinger. “Nonclassicality of induced coherence without induced emission.” Physical Review A 100, no. 5 (2019): 053839.
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
