Author: Ronen Shekel
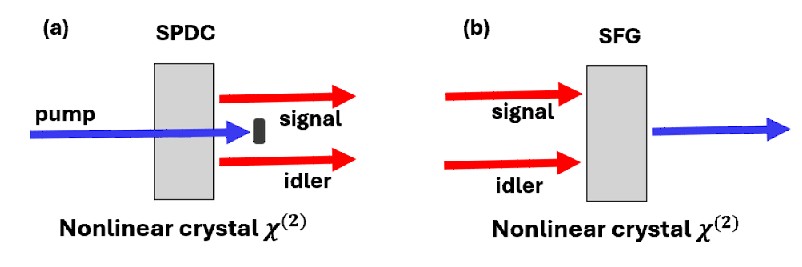
The Hong-Ou-Mandel (HOM) effect is a cornerstone of modern quantum optics. Originally proposed and demonstrated in 1987 by Chung-Ki Hong, Zhe-Yu Ou, and Leonard Mandel from the University of Rochester [1], the HOM effect considers a simple experiment, where two identical photons enter two ports of a beam splitter. A typical way to generate two such single photons is by using nonlinear crystals, such as PPKTP or BBO.
If one merely measures the number of photons at each output port, both ports will show on average the same counts. However, when measuring coincidence events, where photons arrive at both output ports simultaneously, one finds a quantum interference effect. We notice that there are two possible paths that result with a coincidence event: either both pass the beam splitter, or both are reflected (Fig. 1, left). Since each reflection contributes a factor of i to the phase, these two undistinguishable events have opposite phases and interfere destructively, such that no coincidence events will be measured!
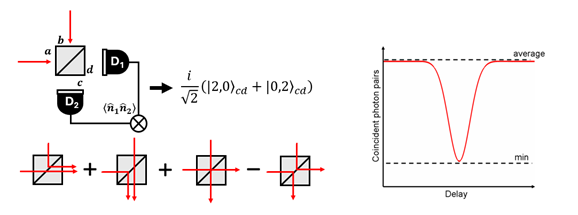
Note however, that for this interference to occur, the two photons must be completely indistinguishable. If one photon enters the beam splitter a long time after the other (longer than the coherence time of the photons), we will obviously know which photon we are measuring at each detector, and the two states will not interfere destructively. If the photons pass the beam splitter with only a slight delay between them, and their wave packets overlap (photons are not little balls! [2]), the destructive interference will occur, but with lower visibility. This is the origin of the famous “HOM dip” (Fig. 1, right), where scanning the delay between the two incoming photons results in a dip in the output coincidence counts.
In fact, in the original HOM paper, this effect was suggested as a means to measure sub-picosecond delays between the two photons, and by implication the length of the photon wave packet, with very high accuracy. Since then, the HOM effect has been used in many different contexts [3], and in particular for characterizing single photon sources such as SPDC [4] or quantum dots [5]: the depth of the HOM dip is a measure of the distinguishability between two single photons, while the width of the dip reflects the photons’ coherence length.
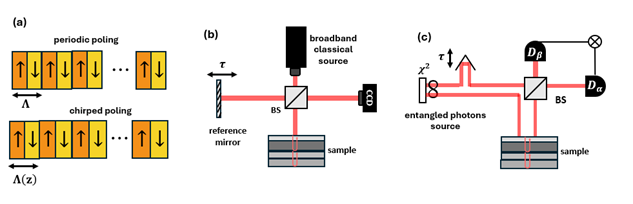
Recently, the HOM effect has been utilized in the context of imaging, where the HOM interference is used to reconstruct the surface depth profile of transparent samples [6]. Identical photons generated using nonlinear crystals and SPDC enter a beam-splitter, where one of the photons first passes through a sample. The different thickness of different areas of the sample induces different delays between the two photons entering the beam-splitter. As discussed above, this will result in a different number of coincidence counts, due to the HOM effect. Thus, the coincidence counts in different pixels of the detectors will reflect the corresponding thickness profile of the sample!
Compared with approaches using classical interference, HOM interference does not require phase stability of the setup, yet it can achieve similar thickness-resolution sensitivity of 1–10 nm.
Other quantum imaging modalities using single and entangled photons, N00N states, or squeezed light provide further advantages, such as sub-shot-noise measurements, better phase sensitivity, and enhanced resolution [7-9].
Besides nonlinear crystals, Raicol is currently developing entangled photon sources, which show excellent HOM visibility, and offer a complete solution for indistinguishable photons. Please contact us for more information!
[1] Hong, Chong-Ki, Zhe-Yu Ou, and Leonard Mandel. “Measurement of subpicosecond time intervals between two photons by interference.” Physical review letters 59.18 (1987): 2044.
[2] Lamb, Willis E. “Anti-photon.” Applied Physics B 60 (1995): 77-84.
[3] Bouchard, Frédéric, Alicia Sit, Yingwen Zhang, Robert Fickler, Filippo M. Miatto, Yuan Yao, Fabio Sciarrino, and Ebrahim Karimi. “Two-photon interference: the Hong–Ou–Mandel effect.” Reports on Progress in Physics 84, no. 1 (2020): 012402.
[4] Kaltenbaek, Rainer, Bibiane Blauensteiner, Marek Żukowski, Markus Aspelmeyer, and Anton Zeilinger. “Experimental interference of independent photons.” Physical review letters 96, no. 24 (2006): 240502.
[5] Sanaka, Kaoru, Alexander Pawlis, Thaddeus D. Ladd, Klaus Lischka, and Yoshihisa Yamamoto. “Indistinguishable photons from independent semiconductor nanostructures.” Physical Review Letters 103, no. 5 (2009): 053601.
[6] Ndagano, Bienvenu, Hugo Defienne, Dominic Branford, Yash D. Shah, Ashley Lyons, Niclas Westerberg, Erik M. Gauger, and Daniele Faccio. “Quantum microscopy based on Hong–Ou–Mandel interference.” Nature Photonics 16, no. 5 (2022): 384-389.
[7] Dowling, Jonathan P., and Kaushik P. Seshadreesan. “Quantum optical technologies for metrology, sensing, and imaging.” Journal of Lightwave Technology 33, no. 12 (2015): 2359-2370.
[8] Moreau, Paul-Antoine, Ermes Toninelli, Thomas Gregory, and Miles J. Padgett. “Imaging with quantum states of light.” Nature Reviews Physics 1, no. 6 (2019): 367-380.
[9] Bowen, W. P., Helen M. Chrzanowski, Dan Oron, Sven Ramelow, Dmitry Tabakaev, Alex Terrasson, and Rob Thew. “Quantum light microscopy.” Contemporary Physics (2023): 1-25.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.