keren, Author at Raicol Crystals

Electro-Optic Modulators: RTP vs. BBO Architectures

High-repetition-rate Q-switching, pulse picking, and cavity dumping require electro-optic modulators that resist piezoelectric ringing and thermal depolarization under high-average-power pumping. This application note sets out the selection criteria for Pockels cells across Raicol’s electro-optic portfolio — specifically focusing on Rubidium Titanyl Phosphate (RTP) and Beta-Barium Borate (BBO) – to support megahertz-regime operation and ultraviolet (UV) laser cavities. All specifications quoted are Raicol catalogue values.

1. The Acoustic Ringing Barrier in MHz Cavities

In megahertz-regime laser cavities, the primary design barrier for electro optic modulation is acoustic (piezoelectric) ringing. When conventional materials (e.g., KD*P or LiNbO₃) are driven by high-repetition-rate electrical pulses, mechanical resonances are excited within the bulk crystal lattice, severely degrading the optical contrast ratio and destabilizing the Q-switch pulse train.

To achieve stable, ringing-free amplitude modulation above 100 kHz, optical architects must transition to crystalline structures possessing minimal piezoelectric coupling coefficients and high acoustic velocities, specifically RTP, which offers ringing-free operation at repetition rates above 1 MHz across its 500–3000 nm operational range. For UV/DUV cavities, BBO provides deep-UV transmission and a very high damage threshold, with ringing-free operation up to ~25 kHz per Raicol’s EO comparison data.

2. RTP & BBO Electro-Optic Specification Comparison

Technical Reference Table: The following empirical specifications are provided for systems architects specifying electro-optic modulators. All values below are Raicol catalogue specifications.

RTP Pockels Cell Specifications

Parameter / Metric	Raicol RTP Pockels Cell
Transparency Range	500 – 3000 nm
Acoustic / Piezoelectric Ringing	None up to the MHz regime (>1 MHz repetition rates)
Half-Wave Voltage (Vπ)	3.6 kV (@ 1064 nm, for EO cell size 9 × 9 × 10 mm²)
LIDT (1064 nm, 10 ns, 10 Hz)	> 1 GW/cm², typical > 2 GW/cm²
Hygroscopic	No (No sealed housing required)
Extinction Ratio (Contrast)	> 35 dB (at 1064 nm)
Primary Applications	High-rep-rate Q-switching, aerospace LIDAR, pulse picking

BBO Pockels Cell Specifications

Parameter / Metric	Raicol BBO Pockels Cell
Transparency Range	Deep-UV transparent; phase matching from 190 to 1780 nm (SHG, SFG, OPO)
Acoustic / Piezoelectric Ringing	Low; ringing-free up to ~25 kHz (Raicol EO comparison data)
LIDT (1064 nm, 10 ns, 10 Hz)	5 GW/cm² @ 1064 nm; 1 GW/cm² @ 532 nm (10 ns pulses)
Hygroscopic	Yes (Requires sealed housing)
Extinction Ratio (Contrast)	> 30 dB (≥ 1000:1)
Primary Applications	UV Q-switching, high-average-power cavities, regenerative amplifiers

*Selection summary: Choose RTP for megahertz-regime repetition rates, low operational voltage, and ruggedized non-hygroscopic packaging; choose BBO for high-power UV/DUV applications and peak damage threshold requirements.

3. Advanced Electro-Optic Manufacturing & Assembly

The operational limits of a Pockels cell are defined not just by the raw crystal, but by the mechanical and geometric assembly. Raicol manufactures advanced configurations to support strict electro-optic tolerances:

Dual-Crystal RTP Thermal Compensation: Because RTP exhibits natural birefringence, its phase retardation is highly sensitive to ambient temperature fluctuations. Raicol manufactures a monolithic-style dual-crystal configuration, precisely matching two RTP elements and mounting them in series with orthogonal crystallographic orientations. This optical architecture internally cancels the natural birefringence and thermal drift, creating a highly temperature-stable modulator while significantly reducing the required driving voltage (Vπ).
Thermally Managed BBO Housings: To support kW-class average power systems without inducing thermal depolarization, Raicol supplies BBO cells integrated into specialized conductive or active water-cooled housings. This structural management dissipates localized heat accumulation away from the optical aperture.
Ruggedized & Dry Packaging: Taking advantage of RTP’s non-hygroscopic lattice, Raicol manufactures dry-packaged Pockels cells without index-matching fluids or hermetically sealed windows. This reduces internal insertion losses and supports packaging requirements for demanding aerospace and defense environments.

4. Design Considerations in Electro-Optic Cavities

Aperture vs. Voltage Trade-offs: In transverse Pockels cells, the half-wave voltage (Vπ) scales directly with the ratio of the crystal aperture (distance between electrodes) to its optical length. Architects must carefully balance the required beam diameter against the voltage limits of their available fast-switching electronics.
Thermal Lensing and Depolarization: At high average powers, residual bulk absorption causes a radial thermal gradient. This induces thermal lensing and spatially varying birefringence, which degrades the extinction ratio. Careful consideration of the crystal’s thermal conductivity and active housing cooling is required for continuous operation.
Treat the Coating as a First-Class Failure Mode: In nanosecond Q-switched regimes, the optical coating commonly fails before the bulk crystal. Raicol supplies highly controlled Ion Assisted Deposition (IAD) AR coatings, which must be specified exactly against the operational wavelength and peak power density of the specific cavity.

5. Engineering Consultation

Raicol’s application engineering team supports optical architects and R&D groups with custom aperture sizing, dual-crystal thermal compensation design, Vπ scaling, and specialized AR coating specification for Q-switching, pulse picking, and cavity dumping systems. Custom electrode configurations and ruggedized housings are available on request.

Raicol Ltd. · 22 HaMelacha St., Rosh HaAyin, Israel · info@raicol.com · www.raicol.com

Crystal Selection for Difference Frequency Generation

Difference Frequency Generation offers a robust, solid-state route to coherent and widely tunable mid-infrared radiation without cryogenic cooling. This application note sets out the crystal selection criteria for DFG cavities across Raicol’s quasi-phase-matched portfolio – periodically poled stoichiometric lithium tantalate (ppSLT), MgO:PPLN and ppKTP – and explains where high gray-track resistance KTP belongs in a high-average-power system. All specifications quoted are Raicol catalogue values.

1. Why DFG for the Mid-Infrared

Demand for widely tunable mid-IR sources continues to grow across spectroscopic environmental sensing, defence and security systems, and non-destructive industrial process control. Direct-emitting semiconductor sources in this spectral region are frequently limited in output power and thermal stability, which makes nonlinear parametric conversion an attractive architectural alternative.

In Difference Frequency Generation, a high-frequency pump at ω₁ and a lower-frequency signal at ω₂ interact within a non-centrosymmetric crystal to generate an idler at the difference frequency:

ω₃ = ω₁ − ω₂ (equivalently 1/λ₃ = 1/λ₁ − 1/λ₂)

For macroscopic energy transfer from the pump and signal fields into the idler, the relative phase velocity of the interacting waves must remain locked over the interaction length. How that condition is met – and what it costs – determines the crystal choice.

2. Quasi-Phase Matching versus Birefringent Phase Matching

In birefringent phase matching, velocity matching relies on crystal anisotropy. This restricts operation to lower effective nonlinear tensor elements and introduces spatial walk-off, which limits the useful interaction length and degrades the output beam quality.

Quasi-phase matching removes both constraints. By periodically inverting the ferroelectric domains with an engineered period Λ, the accumulated phase mismatch is reset before it can reverse the direction of energy flow. Walk-off is eliminated, interaction remains collinear over the full crystal length, and the design is free to access the diagonal element of the nonlinear tensor rather than the weaker off-diagonal terms. The poling period can be engineered during fabrication, so phase matching is set by design rather than by the accident of a crystal’s birefringence.

Figure 1 – spatial walk-off in birefringent phase matching compared with collinear interaction in a periodically poled crystal of domain period Λ.

3. Selecting a QPM Crystal for Mid-IR DFG

ppSLT – periodically poled stoichiometric lithium tantalate

ppSLT is Raicol’s primary QPM material for high-power frequency conversion across an exceptionally broad range, from the ultraviolet to the mid-infrared. Its transparency window of 300–5000 nm covers the full mid-IR band of interest for DFG, and it combines a strong nonlinear coefficient above 7.5 pm/V with high photorefractive damage resistance and excellent thermal conductivity.

The practical consequence is power handling. ppSLT supports more than 10 W of green generation and carries a laser-induced damage threshold of ≥ 570 MW/cm² at 1064 nm, 10 ns, 10 Hz — substantially above MgO:PPLN – which makes it the appropriate choice where the pump is a high-average-power near-IR source and the system cannot tolerate photorefractive lensing.

MgO:PPLN – where nonlinearity dominates

MgO:PPLN offers the highest nonlinear coefficient in the portfolio, with d33 of approximately 27 pm/V, and a transparency range of 420–5200 nm that extends slightly further into the infrared than ppSLT. Its absorption coefficient below 0.1/cm at 1064 nm and compact, integrable geometry suit low- to moderate-power solid-state systems, nonlinear spectroscopy and quantum light sources.

The trade-off is damage threshold. At 100 MW/cm² (1064 nm, 10 ns), MgO:PPLN sits well below ppSLT, so it is best matched to configurations where conversion efficiency per watt matters more than absolute power handling.

ppKTP – broad phase-matching flexibility

ppKTP can be tailored to any nonlinear interaction within the transparency range of KTP, free of the phase-matching limitations of bulk KTP, with an effective nonlinear coefficient roughly three times that of the bulk material. Its transparency of 350–4000 nm covers DFG into the near and lower mid-IR, and it operates near room temperature. With a damage threshold of 600 MW/cm² at 1064 nm for 10 ns pulses and apertures from 1 × 2 up to 2 × 10 mm², it is the most flexible option where the target idler wavelength lies below 4 µm.

4. QPM Specification Comparison

All values below are Raicol catalogue specifications.

Parameter	ppSLT	MgO:PPLN	ppKTP
Transparency range	300 – 5000 nm	420 – 5200 nm	350 – 4000 nm
Nonlinear coefficient	> 7.5 pm/V	d33 ≈ 27 pm/V	approx. 3× bulk KTP
LIDT (1064 nm, 10 ns)	≥ 570 MW/cm²	100 MW/cm²	600 MW/cm²
Bulk absorption @ 1064 nm	190 ppm/cm	< 0.1 /cm	See datasheet
Max length	Up to 40 mm	Up to 40 mm	Up to 30 mm
Typical aperture	0.5 × 2 mm	Up to 1 × 5 mm²	1 × 2 to 2 × 10 mm²
Photorefractive resistance	High	Relatively high	Near room-temperature operation
Typical applications	SHG, SFG, DFG, OPO, THG, FHG	Frequency conversion, spectroscopy, quantum sources	SHG, SFG, DFG, OPO, SPDC

Selection summary: choose ppSLT for high-average-power mid-IR DFG and the broadest transparency; MgO:PPLN where nonlinear efficiency at moderate power is the priority; ppKTP where phase-matching flexibility and aperture options matter and the idler lies below 4 µm.

5. High Average Power: Where HGTR KTP Belongs

A DFG or SHG stage driven at high repetition rate accumulates a different kind of damage from single-shot catastrophic failure. Gray tracks form when a KTP crystal is subjected to high-power, high-repetition-rate pulses or CW irradiation. Induced colour centres absorb broadly across the visible and near infrared, particularly at 532 nm, and because the process is cumulative it progressively degrades harmonic conversion over the life of the system.

Raicol was the first to develop high gray-track resistance flux-grown KTP, enabling higher average power density in SHG across 1000–1400 nm. The distinction matters for system architects: HGTR KTP does not offer a higher peak damage threshold than standard KTP. What it offers is roughly sixteen times the sustainable average power density and an order of magnitude lower gray-track formation – which is what actually determines service life in a continuously operating source.

Parameter	KTP (SHG, OPO)	HGTR KTP
Max aperture	40 × 40 mm²	5 × 5 mm²
Max length	40 mm	15 mm
Bulk absorption	< 100 ppm/cm @ 1064 nm; < 1000 ppm/cm @ 532 nm	< 50 ppm/cm @ 1064 nm; < 150 ppm/cm @ 532 nm
Gray tracking (GRIIRA, 600 s)	2000 ppm/cm	150 ppm/cm
LIDT (1064 nm, 10 ns, 10 Hz)	800 MW/cm²	600 – 800 MW/cm²
Average power density	300 W/cm² @ 1064 nm; 20 W/cm² @ 532 nm	5000 W/cm² @ 1064 nm; 2500 W/cm² @ 532 nm
Typical resistivity	10⁷ Ω·cm	10¹¹ Ω·cm

HGTR KTP additionally offers a nonlinear coefficient four times higher than LBO, a broad temperature bandwidth, small walk-off with wide angular acceptance, and non-hygroscopic handling. Average output power density at 532 nm reaches up to 5 kW/cm² depending on the laser regime.

Design boundary: the aperture and length available in HGTR KTP (5 × 5 mm², up to 15 mm) are smaller than in standard KTP (40 × 40 mm², up to 40 mm). Where large-aperture, high-energy beams are the driving requirement rather than sustained average power, standard KTP remains the correct selection.

6. Advanced Poling Architectures

Beyond the choice of material, the poling pattern itself is a design variable. Raicol supplies ppSLT in fan-out, multi-grating, monolithic and chirped configurations:

Multi-grating structures place several poling periods side by side on a single element, allowing the optimum period to be selected by lateral translation rather than by realignment – and enabling high-power THG on a single element.
Fan-out poling provides continuous tuning for tunable SHG and tunable OPO/OPG, watt-class visible generation, and rapid feasibility testing at new wavelengths.
Monolithic configurations reduce component count and alignment sensitivity in compact systems.
ppSLT waveguides, written by femtosecond laser, deliver an order-of-magnitude increase in conversion efficiency with watt-class operation from the UV and visible through to the mid-IR, and a circular output beam.

7. Design Considerations in DFG Cavities

Specify the poling period against the real operating temperature. A period calculated from a Sellmeier equation without accounting for the actual temperature of the crystal housing will leave residual phase mismatch. Multi-grating elements allow the optimum period to be verified experimentally under real thermal load.
Design for the thermal gradient, not just the average temperature. Residual absorption under high-average-power pumping produces a radial refractive index gradient, inducing thermal lensing and reducing conversion efficiency even in substrates that resist photorefractive damage. Temperature acceptance narrows as crystal length increases, so gain and thermal tolerance must be traded against each other deliberately.
Treat the coating as a first-class failure mode. In nanosecond regimes the optical coating commonly fails before the bulk crystal. Raicol supplies AR/AR, DBAR, TBAR, HR and IBS coatings, including dual-band designs below 0.5% reflectivity, specified against the pump, signal and idler wavelengths of the specific interaction.
Match the crystal to the power regime, not the peak specification. Peak damage threshold governs short-pulse survival; average power density and gray-track resistance govern service life in continuously operating systems. These are different questions and they can point to different crystals.

8. Engineering Consultation

Raicol’s application engineering team supports optical architects and R&D groups with custom poling period design, aperture and length selection, advanced poling patterns, and coating specification for DFG, OPO and harmonic generation systems. Custom apertures and geometries are available on request. Our experts are ready to help you select the optimal solution for your application. Contact Us.

Further Reading

Fejer, M. M., Magel, G. A., Jundt, D. H., & Byer, R. L. “Quasi-phase-matched second harmonic generation: tuning and tolerances.” IEEE Journal of Quantum Electronics, Vol. 28, Issue 11, pp. 2631–2654 (1992).

Kato, K., & Takaoka, E. “Sellmeier and thermo-optic dispersion formulas for KTP.” Applied Optics, Vol. 41, Issue 24, pp. 5040–5044 (2002).

Specifications quoted throughout are taken from the Raicol product catalogue. Values are typical; guaranteed specifications for a given part number are confirmed at order.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Ronen Shekel

Quantum entanglement stands as one of the most profound and practically significant phenomena in modern physics. In communication, entangled photons enable quantum key distribution schemes whose security is guaranteed by the laws of physics, rather than by assumptions about computational hardness. In computation, large entangled states are what allow quantum algorithms such as Shor’s to threaten many of today’s cryptographic standards once scalable quantum processors exist. Many of these applications rely on entangled photon pairs, so having robust and well-controlled sources of entanglement is a central ingredient.

When photon pairs are generated via spontaneous parametric down-conversion (SPDC), certain types of entanglement arise naturally from conservation laws. Energy conservation couples the photon frequencies, yielding time–frequency entanglement. Momentum conservation links their emission directions, creating spatial entanglement. However, polarization is different. Standard nonlinear interactions typically produce pairs with well-defined polarizations, such as |HH> or |HV>, rather than the coherent superposition required for entanglement. To achieve a state like |HH>+|VV>, one must engineer two distinct SPDC processes and erase any distinguishing information (time, spectrum, or spatial mode) that could reveal which process occurred.

From rings and crossed crystals to interferometers

One of the earliest demonstrations was the non-collinear, type-II BBO source by the Zeilinger group in 1995 [1]. Photons emerge on two intersecting cones, one for each polarization (Fig. 1a). By collecting light only from the two overlap regions, the two possible generation paths become indistinguishable. While elegant, this method discards the vast majority of the flux, resulting in low brightness.

To use the full flux of the crystal, collinear schemes were introduced. In the crossed-crystal configuration [2], two thin periodically poled crystals are placed back-to-back with their optic axes rotated by 90° (Fig. 1b). Pumped with a beam at 45° polarization, one crystal generates |HH> pairs and the other |VV> pairs. If these two contributions are made indistinguishable apart from their polarization, the output is a coherent superposition |HH>+|VV>. In practice, additional compensation crystals are needed to erase timing information that may distinguish between the two crystals. Related collinear sources [3] combine a single crystal with a beam splitter and use post-selection at the output, at the cost of half the signal.

A next step was to keep a single crystal but let the pump traverse it twice. In Sagnac interferometer sources [4, 5], the pump enters a polarization Sagnac loop and propagates clockwise and counter-clockwise through the crystal, with each direction generating one of the two processes (Fig. 1c). A “folded sandwich” geometry (Fig. 1d) implements a similar double-pass through a linear interferometer [6]. While these designs produce bright sources, they still rely on interferometers, beam splitters and mirrors that must be aligned and kept mechanically stable.

Figure 1 – Conceptual illustrations of different methods for generating polarization entanglement. All methods implement two SPDC processes made indistinguishable in different ways. (a) Using a non-collinear configuration. (b) Using crossed crystals, each generating photons in a different polarization. (c) A double-pass configuration in a Sagnac interferometer with a polarizing beam-splitter (PBS). (d) A double-pass configuration in a folded sandwich configuration, wich a specially enginnered half waveplate (SWP). (e) Using domain engineering in a single crystal.

Let the poling do the heavy lifting

An alternative approach [7] is to move this complexity inside the nonlinear medium itself (Fig. 1e). By choosing the periodic poling and phase-matching conditions appropriately, a single ppKTP crystal can support both SPDC processes in a single pass, avoiding external interferometers. In a recent collaboration involving Raicol crystals, Shukhin and co-workers improve on this, using a domain-engineered KTP crystal to generate polarization entanglement, and at the same time shape the joint spectral intensity (JSI) [8].

The concept relies on a carefully designed poling pattern that supports two distinct collinear type-II SPDC processes simultaneously. Both processes share the same spatial mode but differ in polarization and frequency. By shaping the phase-matching function via the internal domain structure, the source produces a JSI with circular lobes. This shaping suppresses spectral correlations, rendering the photons spectrally factorable – a critical requirement for high-purity heralded single photons and for entanglement swapping from independent sources. The fact that the properties of the generated photons are dictated by the internal poling structure results in a compact, stable and reliable source that achieves high Bell-inequality violations (S~2.75) and high visibility without post-selection or delicate alignment.

At Raicol, we view this as the evolution of nonlinear crystal technology: moving from simple phase matching to full quantum state engineering. If you are interested in custom domain engineering to tailor entanglement structure or spectral purity, please contact us to discuss the possibilities.

[1] Kwiat, Paul G., Klaus Mattle, Harald Weinfurter, Anton Zeilinger, Alexander V. Sergienko, and Yanhua Shih. “New high-intensity source of polarization-entangled photon pairs.” Physical Review Letters 75, no. 24 (1995): 4337.

[2] Pelton, Matthew, Philip Marsden, Daniel Ljunggren, Maria Tengner, Anders Karlsson, Anna Fragemann, Carlota Canalias, and Fredrik Laurell. “Bright, single-spatial-mode source of frequency non-degenerate, polarization-entangled photon pairs using periodically poled KTP.” Optics Express 12, no. 15 (2004): 3573-3580.

[3] Kuklewicz, Christopher E., Marco Fiorentino, Gaétan Messin, Franco NC Wong, and Jeffrey H. Shapiro. “High-flux source of polarization-entangled photons from a periodically poled KTiOPO 4 parametric down-converter.” Physical Review A 69, no. 1 (2004): 013807.

[4] Weston, Morgan M., Helen M. Chrzanowski, Sabine Wollmann, Allen Boston, Joseph Ho, Lynden K. Shalm, Varun B. Verma et al. “Efficient and pure femtosecond-pulse-length source of polarization-entangled photons.” Optics express 24, no. 10 (2016): 10869-10879.

[5] Kim, Heonoh, Osung Kwon, and Han Seb Moon. “Pulsed Sagnac source of polarization-entangled photon pairs in telecommunication band.” Scientific reports 9, no. 1 (2019): 5031.

[6] Steinlechner, Fabian, Sven Ramelow, Marc Jofre, Marta Gilaberte, Thomas Jennewein, Juan P. Torres, Morgan W. Mitchell, and Valerio Pruneri. “Phase-stable source of polarization-entangled photons in a linear double-pass configuration.” Optics express 21, no. 10 (2013): 11943-11951.

[7] Laudenbach, Fabian, Sebastian Kalista, Michael Hentschel, Philip Walther, and Hannes Hübel. “A novel single-crystal & single-pass source for polarisation-and colour-entangled photon pairs.” Scientific reports 7, no. 1 (2017): 7235.

[8] Shukhin, Anatoly, Inbar Hurvitz, Leonid Vidro, Ady Arie, and Hagai S. Eisenberg. “Direct polarization-entangled photon pair generation using domain-engineered nonlinear crystals.” Optica Quantum 3, no. 5 (2025): 487-494.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Ronen Shekel

Imagine a box with two balls: one red, one blue. Alice takes one ball to Mars and Bob takes the other to Andromeda. The moment Alice opens her box and sees a blue ball: she instantly knows Bob’s is red. This might seem like what Einstein called “spooky action at a distance” [1], but it is not entanglement. This is classical correlation. The properties were fixed from the start.

The Quantum Hallmark: Correlations in Multiple Bases

A hallmark of quantum entanglement is the existence of strong correlations in multiple, incompatible measurement bases [2].

Consider a Bell state, a state in a coherent superposition of horizontal and vertical polarizations, |HH>+|VV>. If Alice and Bob both agree to measure in the H/V basis (for example, by setting their polarizers to 0°/90°), they will find perfect correlations: if Alice gets H, Bob gets H. If she gets V, he gets V. So far, this is just like the red and blue balls.

But if they both agree to switch to an incompatible basis, like the basis of diagonal (D) and anti-diagonal (A) polarization, their results will still be perfectly correlated. This is unique to coherent quantum correlations.

Now, compare this to a simple, non-entangled state, like |HH>. In the H/V basis, their results are perfectly correlated. But if they both measure in the D/A basis, the correlations vanish. The results are random; if Alice measures D, she has no idea if Bob will get D or A.

Bell inequalities are tests designed to measure these very correlations across multiple bases [3, 4]. Rigorous certification of entanglement by violating these inequalities is essential for quantum technologies, from quantum computing to secure communication.

Certifying High-Dimensional Entanglement with SFG

This concept isn’t limited to two-dimensional polarization. As we’ve discussed in a previous post on spatial entanglement, entanglement can be high-dimensional, existing in the spatial properties of photons, where two mutually unbiased bases could be for instance the near-field and far-field distributions. Entanglement could also manifest in the time-energy properties of photon pairs.

In Spontaneous Parametric Down-Conversion (SPDC), a narrowband pump photon splits into two twin photons. Due to energy conservation, the sum of their frequencies ν₁ + ν₂ is precisely fixed. And because they are born at the same instant, the time difference between them (t₁ − t₂) is incredibly small.

For any separable, classical-like state, the uncertainties in these correlated quantities obey a fundamental bound: Δ(t₁ − t₂)Δ(ν₁ + ν₂) ≥ 1⁄2 [5]. A quantum-entangled pair, however, can violate this.

To prove this violation, we cannot simply measure the individual times and frequencies of each photon separately, since doing so would destroy the joint correlation information we seek to certify. Instead, we must perform a global measurement that probes the combined variables (t₁ − t₂) and (ν₁ + ν₂) directly, without accessing the individual values.

Sum-Frequency Generation (SFG) is an ideal tool for this. As the reverse of SPDC (Fig. 1), SFG requires both photons to arrive simultaneously at the crystal, effectively acting as an ultrafast coincidence detector for t₁ − t₂ ≈ 0. Furthermore, it annihilates both photons to create one new photon whose frequency is the sum ν₁ + ν₂, which can then be measured precisely.

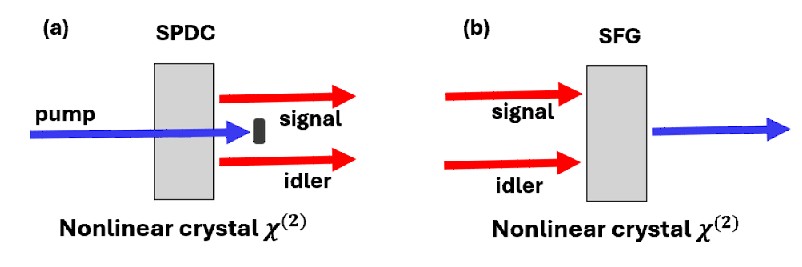
While this idea has been known for years [6, 7], direct SFG with single photons is notoriously inefficient. Recently [8], a groundbreaking experiment from Prof. Avi Pe’er’s group at Bar-Ilan University shattered this barrier, violating the classical bound by an astonishing 12 orders of magnitude. Using a high-quality PPKTP crystal to generate biphotons with an extreme bandwidth of 113 THz, they employed Coherent SFG, where a strong pump stimulates the recombination, to efficiently and directly measure the joint correlation.

The Crystal Connection

The success of such record-breaking work relies on the exceptional quality of nonlinear crystals. At Raicol we are proud to provide such high-quality crystals and are happy to contribute to research pushing the boundaries of quantum science. We are also active participants in international collaborations, such as the European QuantERA project SPARQL, dedicated to advancing quantum technologies.

Time-energy entanglement arises naturally and intrinsically in SPDC through energy conservation – it requires no additional engineering. But how can we engineer entanglement in the polarization degree of freedom? Stay tuned for our next post.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

References

[1] Einstein, A., & Born, M. (1971). Letter from Einstein to Max Born, 3 March 1947. In B. M. Walker (Ed.), The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955 (pp. 157-158). New York.

[2] Giese, Enno. “Entanglement and Its Verification: A Tutorial on Classical and Quantum Correlations.” arXiv preprint arXiv:2511.09507 (2025).

[3] Bell, John S. “On the einstein podolsky rosen paradox.” Physics Physique Fizika 1, no. 3 (1964): 195.

[4] Clauser, John F., Michael A. Horne, Abner Shimony, and Richard A. Holt. “Proposed experiment to test local hidden-variable theories.” Physical review letters 23, no. 15 (1969): 880.

[5] Mei, Yefeng, Yiru Zhou, Shanchao Zhang, Jianfeng Li, Kaiyu Liao, Hui Yan, Shi-Liang Zhu, and Shengwang Du. “Einstein-podolsky-rosen energy-time entanglement of narrow-band biphotons.” Physical Review Letters 124, no. 1 (2020): 010509.

[6] Dayan, Barak, Avi Pe’er, Asher A. Friesem, and Yaron Silberberg. “Nonlinear interactions with an ultrahigh flux of broadband entangled photons.” Physical review letters 94, no. 4 (2005): 043602.

[7] MacLean, Jean-Philippe W., John M. Donohue, and Kevin J. Resch. “Direct characterization of ultrafast energy-time entangled photon pairs.” Physical review letters 120, no. 5 (2018): 053601.

[8] Nechushtan, Nir, Hanzhong Zhang, Yosef London, Mallachi Meller, Haia Amichai, Eliahu Cohen, and Avi Pe’er. “Quantum matched filtering: breaking time-energy separability by 12 orders of magnitude.” arXiv preprint arXiv:2503.03583 (2025).

In modern quantum optics and integrated photonics, precise control over light is essential. Laboratories and industrial applications require devices that offer high speed, stability, and reproducibility. Raicol has established itself as a leading provider of electro-optic devices and nonlinear crystal systems, offering products that enable precise laser modulation, pulse shaping, and frequency conversion for demanding scientific environments. Raicol’s portfolio includes Pockels cells, phase and amplitude modulators, Q-switches, pulse pickers, and a range of advanced nonlinear systems for second harmonic generation (SHG), third harmonic generation (THG), optical parametric oscillation (OPO), and spontaneous parametric down-conversion (SPDC) processes.

Electro-Optic Devices for High-Speed Laser Control

Electro-optic (EO)devices leverage the Pockels effect in nonlinear crystals to modulate laser beams at high speed with nanosecond precision. These devices are central to modern photonics research, enabling scientists to control polarization, phase, and amplitude with exceptional accuracy.

RTP EO Cells and Pockels Cells

Raicol’s RTP (Rubidium Titanyl Phosphate) EO cells are the foundation of their electro-optic product line. RTP belongs to the KTP crystal family and offers outstanding electro-optical properties:

Ultra-fast response: Rise time, fall time, and pulse width < 1 ns
High damage threshold: Over 1 GW/cm² at 1064 nm (typical >2 GW/cm²)
Wide temperature stability: Operating range from -50°C to 70°C
Non-hygroscopic: Easy handling, no protective cover needed
High extinction ratio: >35 dB
Low half-wave voltage: Enables compact design
Minimal acoustic ringing: Compatible for over 1 MHz repetition rate

iRTP Pockels Cells

Raicol’s iRTP (industrial RTP) brings the advantages of RTP to the mass market:

Industrial price point: Standard off-the-shelf solution at competitive pricing
Simplified alignment: Requires only 1-axis alignment vs. 3-axis for KD*P
Thermal stability: 10°C to 50°C operational range without thermal control
High damage threshold: Typically > 1 GW/cm²
Fast response: <1 ns rise time
No acoustic ringing: Up to at least 350 kHz

Applications for EO Devices

Q-Switches: For generating high-energy, short-duration laser pulses
Pulse Pickers: Enabling selection of individual pulses from high-repetition-rate laser trains
Phase Modulators: For precise manipulation of optical phase
Amplitude Modulators: For controlled laser attenuation and modulation
Cavity Dumpers: For extracting stored energy from laser cavities
Optical Shutters: For precise laser beam gating
Attenuators & Deflectors: For beam control applications

Crystal-Based Frequency Conversion Solutions

Raicol offers a comprehensive suite of nonlinear crystal solutions for wavelength conversion, essential for many advanced laser applications.

Second Harmonic Generation (SHG) Crystals

KTP Crystals: The most common nonlinear crystal for SHG of YAG lasers

SHG coefficient approximately three times higher than KDP
High laser damage threshold: 1 GW/cm² at 1064 nm
Large aperture capability: up to 50×50 mm
Excellent thermal stability

HGTR (High Gray Track Resistance) KTP: For high-power applications

Average output power density at 532 nm up to 5 kW/cm²
Nonlinear coefficient 4 times higher than LBO
Designed to resist gray track formation at high power

LBO (Lithium Triborate) Crystals:

Super polished surface quality: roughness ≤ 3Å RMS
Very low bulk absorption: up to 2 ppm/cm at 1064 nm
High damage threshold: 2500 MW/cm² at 1064 nm
Wide transparency range: 160-2600 nm

Third Harmonic Generation (THG)

CLBO (Caesium Lithium Borate): Ideal for deep UV applications

Wide transmission range: 180-2750 nm
Enables frequency conversion below 200 nm
Applications: 4th and 5th harmonics of Nd:YAG, 7th and 8th harmonics of 1550 nm

Optical Parametric Oscillation (OPO)

KTP OPO Crystals: Most efficient for converting 1064 nm to 1572 nm (“eye safe”)

Non-critical phase matching (NCPM) for 1572 nm with no walk-off
Available in monolithic configurations with 20-30% higher efficiency
Apertures up to 40×40 mm, lengths up to 40 mm

Quantum Applications - PPKTP and Beyond

PPKTP (Periodically Poled KTP): Raicol pioneered this technology over 20 years ago

Quasi-phase matching (QPM) enables efficient SPDC processes
Three times larger effective nonlinear coefficient than bulk KTP
Type-0 or Type-II phase matching options
Broad pumping range: 405 nm, 532 nm, 775 nm

HP-APKTP (High Purity Aperiodically Poled KTP):

Aperiodic poling shapes the joint spectrum of SPDC
Higher spectral purity without external filters
Improved Hong-Ou-Mandel visibility compared to standard ppKTP
Type-2 crystal suitable for Ti-Sapphire laser pumping (775-795 nm)

PPKTP Innovations:

Waveguides: 23× higher nonlinear efficiency compared to bulk crystals
Monolithic crystals: Mirror-coated facets for squeezed light generation
2D poling: For spatial qudit generation and quantum holography
Short poling periods: Down to 1.2 μm for narrow-band counter-propagation SPDC

Integrated Photonics and Future Technologies

Raicol is developing advanced solutions for integrated photonics:

Waveguide Technologies

ppKTP waveguides: Enhanced pair generation efficiency (>10× bulk efficiency)
RTP waveguide modulators: For integrated photonic applications
Thin film RTP: Optimized for silicon photonics integration

Quantum Components

Heralded Single-Photon Modules: Fiber-coupled, integrated with thermal control
Entangled Photon Sources: Sagnac-loop design with >95% visibility
Squeezed Light Sources: Monolithic ppKTP for quantum sensing

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Ronen Shekel

Even the most stable laser isn’t perfectly quiet. The fact that light comes in discrete photons introduces statistical fluctuations known as shot noise, leading to the standard quantum limit for optical measurement precision.

However, quantum optics provides a workaround. A squeezed state redistributes uncertainty, shrinking noise in one property (phase or amplitude) below the shot‑noise floor while increasing it in the other. On a phase-amplitude diagram the round noise circle turns into an elongated ellipse. Such engineered low-noise light boosts the sensitivity of LIGO’s gravitational‑wave detectors [1], squeezed‑light magnetometers [2], and many other quantum sensing and communication applications.

A common method to generate squeezed light is through a Degenerate Optical Parametric Amplifier (DOPA). In a DOPA, a strong pump laser beam interacts with a nonlinear crystal, typically placed inside an optical cavity to enhance the interaction, and drives the generation of photon pairs. The phase‑sensitive nature of the process allows the cavity to reduce fluctuations along one quadrature while amplifying the orthogonal one. The strength of this interaction is characterized by its effective nonlinear coefficient; a higher value usually indicates a more efficient conversion process, which can translate to stronger squeezing for a given crystal length and pump power.

The Crystal Choice: Operating Temperature and Intrinsic Noise

Two prominent nonlinear materials for constructing DOPAs are periodically poled Potassium Titanyl Phosphate (PPKTP) and periodically poled Lithium Niobate (PPLN). PPLN has a higher nonlinear coefficient than PPKTP, suggesting it is inherently better for generating strong squeezing. However, practical operational requirements introduce crucial differences.

PPLN often suffers from a photorefractive effect when exposed to high-intensity laser light near room temperature. This effect involves the light-induced generation and migration of charge carriers within the crystal, creating internal electric fields that distort the crystal’s refractive index and degrade the quality of the transmitted laser beams. To mitigate photorefraction, PPLN-based devices are typically operated at high temperatures, such that the trapped charges have enough energy to become mobile again, averaging out the internal fields and mitigating the effect. In contrast, PPKTP-based DOPAs can operate efficiently near room temperature without significant photorefractive problems.

This difference in operating temperature has significant consequences for the ultimate noise performance. At elevated temperatures, the atomic lattice vibrates, resulting in microscopic acoustic waves propagating through the crystal. These waves randomly modulate the refractive index. This phenomenon, known as Guided Acoustic Wave Brillouin Scattering (GAWBS), introduces a fundamental source of phase noise that is directly dependent on the crystal’s temperature [3].

A direct experimental comparison by Wan et al. highlighted this critical trade-off [4]. Using identical 1550 nm DOPA setups, they found 6.8 dB of squeezing – that is, 6.8 dB of noise reduction below the standard quantum limit – for room-temperature PPKTP versus 4.9 dB using PPLN at 135°C. The superior squeezing performance of PPKTP, despite its lower nonlinear coefficient, was directly attributed to the reduced GAWBS-induced phase noise at its cooler operating temperature.

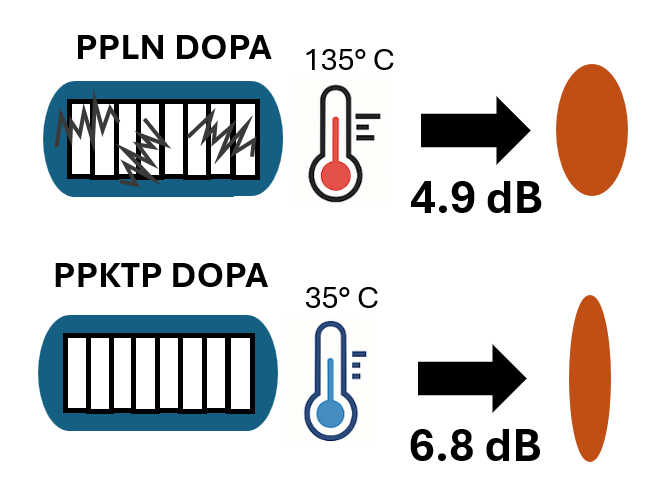
For the strongest phase squeezing, eliminating GAWBS matters more than the absolute value of the nonlinear coefficient. Indeed, record squeezing levels of 12 dB at 1550 nm and 15 dB at 1064 nm both used PPKTP [5, 6], underlining its exceptional low-noise properties.

Raicol: Precision Crystals for Quantum Light

Deep squeezing requires crystals with precisely controlled poling, ultralow absorption, and exceptional uniformity. Raicol’s PPKTP crystals are engineered to these exacting standards, with options for custom periodicities and aperiodic poling designs. For your next squeezed light source, we invite you to explore our products and consult with our team to identify the optimal crystal configuration for your specific applications.

References

[1] Aasi, Junaid, Joan Abadie, B. P. Abbott, Richard Abbott, T. D. Abbott, M. R. Abernathy, Carl Adams et al. “Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light.” Nature Photonics 7, no. 8 (2013): 613-619.

[2] Wolfgramm, Florian, Alessandro Cere, Federica A. Beduini, Ana Predojević, Marco Koschorreck, and Morgan W. Mitchell. “Squeezed-light optical magnetometry.” Physical review letters 105, no. 5 (2010): 053601.

[3] César, Jônatas Eduardo da Silva, A. S. Coelho, Katiuscia Nadyne Cassemiro, Alessandro de Sousa Villar, M. Lassen, P. Nussenzveig, and Marcelo Martinelli. “Extra phase noise from thermal fluctuations in nonlinear optical crystals.” Physical Review A—Atomic, Molecular, and Optical Physics 79, no. 6 (2009): 063816.

[4] Wan, Zhenju, Jinxia Feng, Yuanji Li, and Kuanshou Zhang. “Comparison of phase quadrature squeezed states generated from degenerate optical parametric amplifiers using PPKTP and PPLN.” Optics express 26, no. 5 (2018): 5531-5540.

[5] Mehmet, Moritz, Stefan Ast, Tobias Eberle, Sebastian Steinlechner, Henning Vahlbruch, and Roman Schnabel. “Squeezed light at 1550 nm with a quantum noise reduction of 12.3 dB.” Optics express 19, no. 25 (2011): 25763-25772.

[6] Vahlbruch, Henning, Moritz Mehmet, Karsten Danzmann, and Roman Schnabel. “Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency.” Physical review letters 117, no. 11 (2016): 110801.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Ronen Shekel

Building large-scale quantum networks hinges on connecting different quantum systems, but these often operate at distinct optical wavelengths. Nitrogen-vacancy centers in diamond, for instance, are excellent candidates for quantum network nodes, emitting single photons at 637 nm [1].

However, transmitting these photons efficiently over long distances through standard optical fibers is problematic, as 637 nm light suffers significant loss. Conversion to the low-loss telecommunication bands is therefore essential.

Quantum frequency conversion (QFC) provides the solution, coherently shifting the wavelength of quantum light while preserving its crucial quantum properties, like entanglement or squeezing. Despite progress, achieving efficient QFC without introducing significant noise has remained a major challenge [2].

Even small amounts of noise can degrade or destroy the fragile quantum states, severely limiting quantum communication and networking capabilities.

A promising new platform, recently demonstrated by Mann et al. [3] using a crystal supplied by Raicol, utilizes a monolithic bulk ppKTP cavity. A “monolithic” cavity means the reflective mirrors forming the optical resonator are coated directly onto the crystal’s end facets, creating a single, integrated device.

This innovative design dramatically boosts the effective power of a modest, off-the-shelf 1064 nm pump laser circulating inside it. The enhanced pump power then efficiently drives the difference frequency generation (DFG) process needed to convert 637 nm photons to the telecom C-band (around 1587 nm in their work), while keeping the generation of unwanted noise photons remarkably low (Fig. 1).

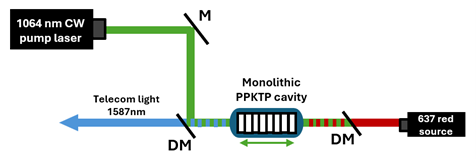
The Power of Monolithic Cavities

Efficient QFC in bulk crystals typically requires high pump powers, often necessitating expensive and complex laser systems. Resonant cavities offer a clever workaround, building up intense light fields inside the crystal from modest input powers. The monolithic design offers specific advantages: it is inherently compact and robust. Furthermore, these cavities can exhibit passive thermal self-tuning [4], meaning they can naturally stay on resonance without needing active electronic feedback loops.

This simplification significantly enhances reliability and practicality for real-world network deployment. Mann et al. [3] also hypothesize that a key advantage comes from using bulk ppKTP: the high quality of periodic poling achievable in bulk KTP [5] may intrinsically suppress parasitic nonlinear processes, particularly unwanted spontaneous parametric down-conversion (SPDC) originating from the strong pump – a major noise source in other QFC approaches.

Record Low Noise and Quantum State Preservation

The Path Forward

The Mann et al. experiment achieved an impressive internal conversion efficiency of up to 72% using only a 3 W input pump laser. Even more significantly, the noise generated was exceptionally low, measured at approximately 110 kHz/nm – a figure quantifying the rate of unwanted noise photons generated per nanometer of bandwidth at the target wavelength. This result represents a 5-fold noise reduction compared to the previous best state-of-the-art single-step converters operating at these wavelengths, dramatically increasing the feasibility of realistic quantum communication links.

Preserving the quantum nature of the light through the conversion process is crucial. The team rigorously verified this by converting single photons from an entangled pair source (SPDC). Measurements of the second-order correlation function confirmed the preservation of non-classical correlations, showing behaviour far exceeding classical limits. They also performed Franson interferometry and a chained Bell inequality test, demonstrating convincingly that time-energy entanglement was preserved with high fidelity through the conversion process.

This work highlights the significant potential of monolithic bulk ppKTP cavities as a robust, efficient, and remarkably low-noise platform for quantum network wavelength conversion. At Raicol Crystals, we provide the high-quality nonlinear crystals essential for this work, including ppKTP, apKTP, and monolithic PPKTP with broadband mirror coatings.

Our expertise in precise periodic and aperiodic poling techniques enables researchers to achieve optimal results in quantum optics applications. We also collaborate with research teams to develop customized monolithic designs that maximize efficiency while maintaining ultra-low noise profiles.

Our ongoing development of narrowband photon sources represents our commitment to advancing quantum technology. Contact Raicol Crystals to explore how our crystals can support your quantum research objectives and help bridge critical wavelength gaps in your experimental systems.

References

[1] Ruf, Maximilian, Noel H. Wan, Hyeongrak Choi, Dirk Englund, and Ronald Hanson. “Quantum networks based on color centers in diamond.” Journal of Applied Physics 130, no. 7 (2021).

[2] Dréau, Anaïs, Anna Tchebotareva, Aboubakr El Mahdaoui, Cristian Bonato, and Ronald Hanson. “Quantum frequency conversion of single photons from a nitrogen-vacancy center in diamond to telecommunication wavelengths.” Physical review applied 9, no. 6 (2018): 064031.

[3] Mann, Felix, Helen M. Chrzanowski, Felipe Gewers, Marlon Placke, and Sven Ramelow. “Low-noise quantum frequency conversion in a monolithic cavity with bulk periodically poled potassium titanyl phosphate.” Physical Review Applied 20, no. 5 (2023): 054010.

[4] Zielińska, Joanna A., and Morgan W. Mitchell. “Self-tuning optical resonator.” Optics letters 42, no. 24 (2017): 5298-5301.

[5] Mann, Felix, Helen M. Chrzanowski, and Sven Ramelow. “Low random duty-cycle errors in periodically poled KTP revealed by sum-frequency generation.” Optics Letters 46, no. 13 (2021): 3049-3052.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Ronen Shekel

Spontaneous parametric down-conversion (SPDC) is a cornerstone of quantum optics, enabling the generation of entangled photon pairs with remarkable properties. One such property, dispersion cancellation, reveals how entanglement can mitigate effects that typically distort light as it travels through materials. This phenomenon, first explored in the early 1990s, offers both fundamental insights into quantum mechanics and practical applications in quantum technologies. In this post, we discuss how dispersion affects light, how entanglement counters it, and key experiments that have shaped our understanding.

Classical Dispersion: The Spreading of Light

When a short pulse of classical light travels through a vacuum, it retains its compact shape. However, propagation through a material like glass introduces a phenomenon known as dispersion. In a material, the refractive index varies with wavelength, n≈n₀+β(λ-λ₀ ), where β is the dispersion coefficient at a reference wavelength λ_0, causing different wavelengths of light to travel at different speeds. Since a short pulse comprises a range of wavelengths – owing to its Fourier composition – each component propagates at its own velocity. As a result, the pulse broadens over time.

In materials exhibiting normal dispersion, longer wavelengths (lower frequencies) tend to move faster, while in those with anomalous dispersion, shorter wavelengths (higher frequencies) take the lead. In either case, the outcome is the same: the initially sharp pulse spreads out, losing its compact temporal profile. This effect poses challenges for applications requiring precise timing or short pulses.

Franson’s Nonlocal Dispersion Cancellation

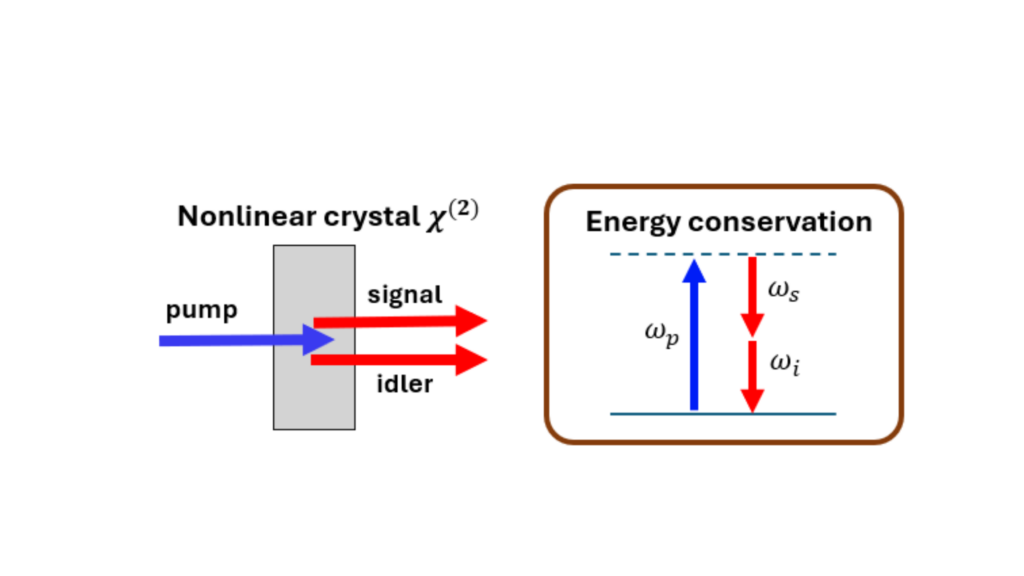
Consider now a pair of spectrally entangled photons generated via SPDC in a nonlinear crystal. A narrowband pump beam splits into two photons – signal and idler – whose frequencies are tightly correlated due to energy conservation (Fig. 1). When measured jointly, their arrival-time correlations are related to the temporal width of their wave-packets, set by their spectral bandwidth via the Fourier transform. But what happens when these photons travel through dispersive media, where dispersion smears each wave-packet and broadens their correlations?

In 1992, J.D. Franson proposed an intriguing experiment (Fig. 2a). He suggested sending each photon through a different dispersive medium – one with normal dispersion, the other with anomalous dispersion – and then measuring their joint arrival times. Classically, one might expect the dispersion to broaden each photon’s wave-packet, resulting in a wider correlation profile. Surprisingly, Franson found that when the dispersions are opposite in sign, the broadening cancels out. The correlation remains as narrow as it was without dispersion!

This effect arises from the entangled nature of the photon pair. The joint two-photon state ensures that the dispersion experienced by one photon is precisely counteracted by that of its twin, a phenomenon described as nonlocal because the photons need not interact directly, and the two detectors might be very far away from each other. While classical analogs to this experiment exist [2], this cancellation highlights a distinctly quantum feature tied to entanglement, as the photons’ individual distortions are reconciled only through their shared state [3].

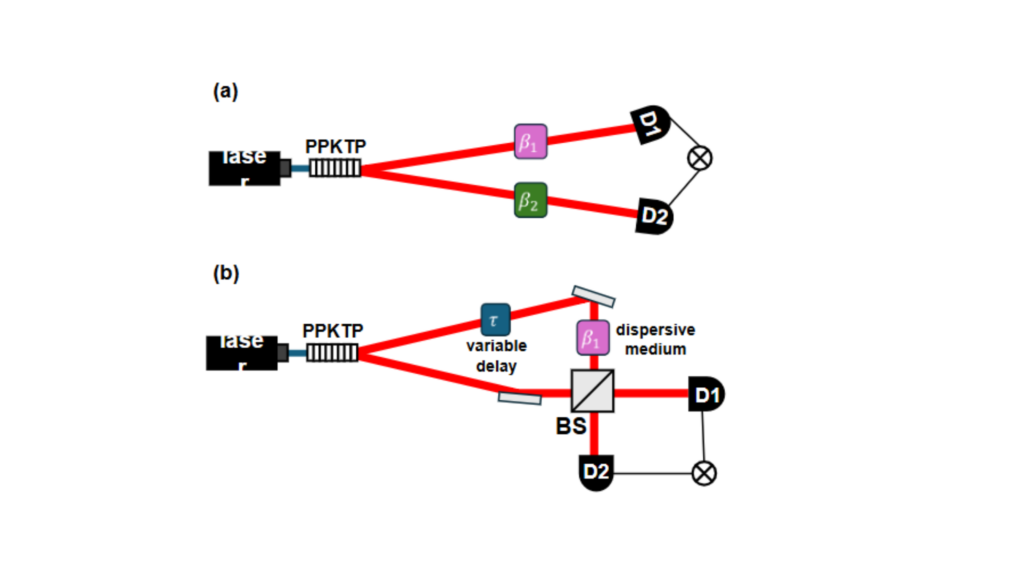
Figure 2. (a) The Franson dispersion cancellation setup, where two entangled photons propagate through different dispersive media β_1,β_2 and are measured via single photon detectors D1, D2 which may be very far away from each other. (b) The Steinberg local dispersion cancellation setup, where only one of the photons propagates through a dispersive medium and a variable delay, and where both photons are then combined in a Hong-Ou-Mandel interferometer.

Steinberg’s Local Dispersion Cancellation

Shortly after Franson’s work, Aephraim Steinberg and colleagues proposed a complementary approach [4, 5]. In their experiment, only one of the entangled photons passes through a dispersive medium, while the other travels freely. The photons are then reunited at a beam splitter in a Hong-Ou-Mandel (HOM) interferometer (Fig. 2b), where identical photons exhibit a characteristic dip in coincidence counts due to destructive interference. Specifically, if two indistinguishable photons arrive at the beam splitter simultaneously, they will both exit in the same output port, thereby reducing coincidences and producing the HOM dip.

Once again, one might anticipate that dispersion would stretch the affected photon’s wave-packet, thereby reducing the overlap with its twin and broadening the HOM dip. However, Steinberg showed that the dip remains narrow, largely unaffected by the dispersion. This occurs because the two-photon amplitudes along possible paths through the beam splitter interfere in a way that cancels the dispersion’s impact. Remarkably, this setup also provided experimental evidence that a single photon travels through a material at its group velocity – the speed of the wave-packet’s peak – resolving a point of contention in photon propagation studies at the time.

Developments Since the 1990s

Since these pioneering experiments, dispersion cancellation has been explored in multiple contexts. The Franson effect has been demonstrated using diverse measurement methods [6, 7], and the dispersion cancellation concept has been extended to systems such as Mach-Zehnder interferometers [8] and optical cavities [9]. It has also been generalized to three-, or even multi-photon states [10], as well as to independent photons [11]. These advancements underscore the versatility of SPDC-generated photons and their utility in quantum optics research.

Implications and Applications

Dispersion cancellation illustrates how entanglement can preserve the integrity of quantum states against material-induced distortions. This property is valuable for quantum communication, where precise timing is critical, and for quantum imaging, where maintaining narrow correlations enhances resolution. At Raicol Crystals, we specialize in crafting nonlinear crystals that enable such experiments, providing researchers with the tools to explore and harness these effects. For more information on our quantum solutions, visit our quantum components page, or contact us directly.

References

[1] Franson, J. D. “Nonlocal cancellation of dispersion.” Physical Review A 45, no. 5 (1992): 3126.

[2] Shapiro, Jeffrey H. “Dispersion cancellation with phase-sensitive Gaussian-state light.” Physical Review A—Atomic, Molecular, and Optical Physics 81, no. 2 (2010): 023824.

[3] Franson, J. D. “Lack of dispersion cancellation with classical phase-sensitive light.” Physical Review A—Atomic, Molecular, and Optical Physics 81, no. 2 (2010): 023825.

[4] Steinberg, A. M., P. G. Kwiat, and R. Y. Chiao. “Dispersion cancellation in a measurement of the single-photon propagation velocity in glass.” Physical review letters 68, no. 16 (1992): 2421.

[5] Steinberg, Aephraim M., Paul G. Kwiat, and Raymond Y. Chiao. “Dispersion cancellation and high-resolution time measurements in a fourth-order optical interferometer.” Physical Review A 45, no. 9 (1992): 6659.

[6] Baek, So-Young, Young-Wook Cho, and Yoon-Ho Kim. “Nonlocal dispersion cancellation using entangled photons.” Optics express 17, no. 21 (2009): 19241-19252.

[7] O’Donnell, Kevin A. “Observations of dispersion cancellation of entangled photon pairs.” Physical review letters 106, no. 6 (2011): 063601.

[8] Larchuk, Todd S., Malvin C. Teich, and Bahaa EA Saleh. “Nonlocal cancellation of dispersive broadening in Mach-Zehnder interferometers.” Physical Review A 52, no. 5 (1995): 4145.

[9] Agarwal, Girish S., and S. Dutta Gupta. “Filtering of two-photon quantum correlations by optical cavities: Cancellation of dispersive effects.” Physical Review A 49, no. 5 (1994): 3954.

[10] Nodurft, I. C., S. U. Shringarpure, B. T. Kirby, T. B. Pittman, and J. D. Franson. “Nonlocal dispersion cancellation for three or more photons.” Physical Review A 102, no. 1 (2020): 013713.

[11] Im, Dong-Gil, Yosep Kim, and Yoon-Ho Kim. “Dispersion cancellation in a quantum interferometer with independent single photons.” Optics Express 29, no. 2 (2021): 2348-2363.

Author: Ori levin

At Raicol, as a world leader in the manufacture of PPKTP, our goal is to support the growing quantum industry and drive it forward as much as we can.
To support this goal, Raicol is continuously cooperating with research centers and leading universities worldwide to provide them with advanced quasi-phase-matching crystals that help them accomplish innovative research. At times, this requires us to push the envelope to improve our fabrication techniques and bring new capabilities.
In the past few years, Raicol has been dealing with repeating requests for PPKTP with low absorption, higher pump powers, and requests for shorter poling periods. We found some of these requirements intriguing and challenging and started researching different solutions to tackle these issues.

One of the leading challenges our customers face is dealing with gray tracking.
Gray tracking is a phenomenon where optical beams, above the average power threshold, propagate through PPKTP crystal and create photorefractive damage that leaves opaque areas, making the crystal useless.

In unpolled KTP which is used for nonlinear conversions, Raicol solved this issue by developing the HGTR KTP which was designed to support much higher power densities, however, HGTR KTP cannot be easily polled, thus does not offer a solution for the quantum industry.

To tackle this problem, Raicol has started a research project to develop a new product that will support a higher power-frequency conversion process
(such as SPDC) but at the same time, will not compromise the PPKTP absorption parameters. During the research, we have emphasized optimizing the Raicol bulk KTP absorption.

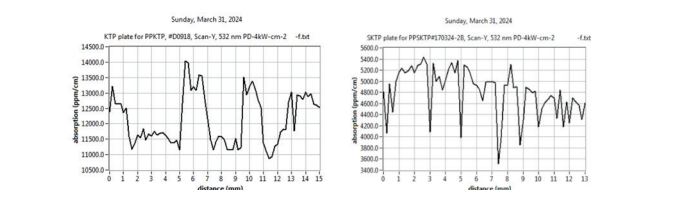
Following two years of research, Raicol developed a version of HGRK KTP that can be polled and created the new version of ppKTP which we called SPPKTP. The SppKTP supports up to 6 times the power as a standard PPKTP and has about 40% less absorption (ppm) in the 532 nm wavelength .

This technology finds numerous applications where even the smallest optical losses are highly detrimental or systems that can benefit from higher powers than typical KTP can support. Key examples include Optical Parametric Oscillators (OPOs), squeezed light sources, Quantum communications and quantum encryption (QKD), and high-power laser systems, where the high circulating power within the optical cavity demands an elevated optical damage threshold, exceptional crystal purity, and minimal losses to maintain efficient frequency conversion. In such systems, even minute losses can lead to reduced performance, thermal effects, and beam quality degradation.

In contrast, there are also applications operating at low power but requiring extremely low optical losses, such as systems with high Q-factor optical cavities. Here, losses directly influence the cavity linewidth, with narrow linewidths being essential for applications in high-precision metrology, laser stabilization, and quantum technologies.

Raicol’s SPPKTP crystals represent a significant advancement in nonlinear optical materials, driving innovation across diverse areas of photonics technology. Their breakthrough properties help unlock new possibilities in the field, from quantum applications to high-power laser systems

For detailed information about our sPPKTP crystals, download our product brochure or reach out to our team.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Ronen Shekel

Quantum and classical ghost imaging

Ghost imaging, one of the first imaging techniques using quantum light, has captivated researchers since its inception in the mid-1990s. The concept of ghost imaging was first demonstrated in 1995 by Pittman et al. [1], using quantum light generated via spontaneous parametric down-conversion (SPDC), a nonlinear optical process that converts a pump photon into two lower-energy entangled photons.

In this experiment (Fig. 1a), the spatially entangled photons are separated, with one photon propagating through an object and being collected using a bucket detector with no spatial resolution, while the idler photon is sent to a multi-pixeled camera. By measuring coincidence events between the bucket detector and the camera, the object is reconstructed, despite the fact that the photons detected by the camera did not directly interact with it! This nonlocal characteristic led to the term “ghost imaging.”

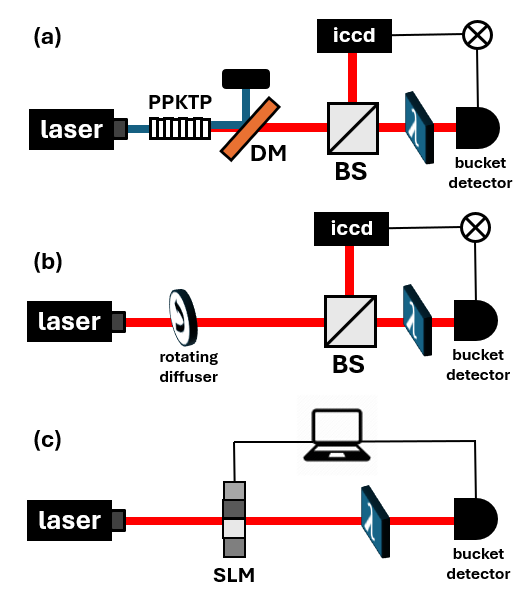
Figure 1 - Three implementations of ghost imaging: (a) Quantum ghost imaging using spatially-entangled photon pairs generated via SPDC. (b) Classical ghost imaging using pseudo-thermal light generated using a laser and a rotating diffuser. (c) Computational ghost imaging utilizing a single detector and calculated field patterns. DM – dichroic mirror, BS – beam-splitter, SLM – spatial light modulator, iccd – intensified charge-coupled device (camera).

The crux of this technique lies in the spatial correlations of the two photons: areas that are blocked by the object will not reach the bucket detector, so coincidence events will not occur with the corresponding pixels in the camera. But one must remember: correlations do not necessarily imply entanglement! Does quantum entanglement play a critical role in this technique? This was the subject of a debate that lasted several years.

In [2], for instance, theoretical arguments were presented, suggesting that entanglement is intrinsic to ghost imaging. However, in 2002, Bennik et al. [3] demonstrated ghost imaging using two classically correlated beams, randomly deflected at different angles. Others explored similar classical correlations using a rotating diffuser [4], generating correlated pseudo-thermal light (Fig. 1b).

Computational ghost imaging

An important fruit of this debate was that of computational ghost imaging, proposed by Shapiro [5], and demonstrated by Bromberg et al. [6]. In this method, only a single detector is used, and the high-resolution camera is replaced by a computation of the propagating field which is shaped using a spatial light modulator (Fig. 1c). The key point here is that we know everything about the photon propagating to the camera, so we can utilize this knowledge computationally and get rid of the physical camera. The object image is obtained by correlating the intensities measured by the bucket detector with the calculated field at the object plane.

While this computational approach already simplified the experimental setup, researchers soon realized [7] that the number of measurements could be significantly reduced by leveraging modern image processing techniques, particularly those that exploit prior knowledge about the image structure. Remarkably, for most imaging tasks, such information exists: natural images are sparse, that is, they contain many coefficients close to or equal to zero when represented in an appropriate basis. This property of natural images is at the core of modern lossy image compression algorithms, such as JPEG. The field of compressed sensing exploits this sparsity/compressibility to reduce the number of measurements needed for faithful image recovery. Utilizing this technique reduces the number of measurements required for a faithful reconstruction by an order of magnitude.

Current state and future directions

The fact that computational ghost imaging uses only a single detector provides experimental evidence that pseudothermal ghost imaging does not inherently rely on nonlocal quantum correlations. It is now also recognized that the quantum and classical methods produce images of a similar resolution. The main advantage of utilizing quantum light for ghost imaging is found at low light levels, at which the quantum modality exhibits greater visibility and a greater signal-to-noise ratio [8]. This could be especially important when imaging samples that are sensitive to high light levels. Further details comparing the classical and quantum modalities may be found in [9].

Almost 30 years since its first demonstration, many extensions, applications, and modalities of ghost imaging are still being explored. Are you interested in ghost imaging with quantum light? Or perhaps want to explore other use cases for quantum entanglement? Please check out our PPKTP crystal and BBO crystals, used for generating entangled photons, and join the conversation!

[1] Pittman, Todd B., Y. H. Shih, D. V. Strekalov, and Alexander V. Sergienko. “Optical imaging by means of two-photon quantum entanglement.” Physical Review A 52, no. 5 (1995): R3429.

[2] Abouraddy, Ayman F., Bahaa EA Saleh, Alexander V. Sergienko, and Malvin C. Teich. “Role of entanglement in two-photon imaging.” Physical review letters 87, no. 12 (2001): 123602.

[3] Bennink, Ryan S., Sean J. Bentley, and Robert W. Boyd. ““Two-photon” coincidence imaging with a classical source.” Physical review letters 89, no. 11 (2002): 113601.

[4] Valencia, Alejandra, Giuliano Scarcelli, Milena D’Angelo, and Yanhua Shih. “Two-photon imaging with thermal light.” Physical review letters 94, no. 6 (2005): 063601.

[5] Shapiro, Jeffrey H. “Computational ghost imaging.” Physical Review A—Atomic, Molecular, and Optical Physics 78, no. 6 (2008): 061802.

[6] Bromberg, Yaron, Ori Katz, and Yaron Silberberg. “Ghost imaging with a single detector.” Physical Review A—Atomic, Molecular, and Optical Physics 79, no. 5 (2009): 053840.

[7] Katz, Ori, Yaron Bromberg, and Yaron Silberberg. “Compressive ghost imaging.” Applied Physics Letters 95, no. 13 (2009).

[8] Moreau, Paul-Antoine, Ermes Toninelli, Thomas Gregory, and Miles J. Padgett. “Imaging with quantum states of light.” Nature Reviews Physics 1, no. 6 (2019): 367-380.

[9] Erkmen, Baris I., and Jeffrey H. Shapiro. “Ghost imaging: from quantum to classical to computational.” Advances in Optics and Photonics 2, no. 4 (2010): 405-450.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Yoad Michael

PPKTP Crystal is a quasi-phased-matched crystal that converts light of one wavelength into a different wavelength. The original purpose of this crystal was humble: It was designed to be an efficient frequency converter for laser system by second harmonic generation. However, with recent advances in quantum optics, the process of spontaneous parametric down conversion (SPDC) is now the dominating application of PPKTP.

SPDC is a process in which a strong pump beam is converted into correlated photon pairs, coined Signal and Idler. These correlations are the basis for various sources of quantum light, such as heralded single photons, time-energy or polarization entangled photon pairs, and squeezed light.

While it is convenient to consider only the quantum properties these light sources, the nonlinear properties of the interaction play a very significant role. For example, in PPKTP, the phase matching can be fully controlled such that: the signal and idler have the same polarization (type-0) or orthogonal polarization (type-2), same wavelength (degenerate) or separate wavelengths (nondegenerate), emitted along the direction of the pump beam (collinear) or at some angle (noncollinear). The type-0/type-2 is determined by the polling period and is something that needs to be determined at the manufacture stage, while degeneracy and collinearity can be fine-tuned by temperature (to avoid working at bizarre temperatures, it is advised to specify these parameters beforehand and adjust the polling period).

We can dive deeper into these differences. Polarization is not the only optical property that changes between type-0 and type-2 interactions; Spectral bandwidth, pair rate, and tolerance to temperature are also different. This is best illustrated by the wonderful work of the Ursin group [1], in which they compared type-0 and type-2 crystals as sources of polarization entangled photon pairs. As shown in Figure. 1, Type-0 is significantly broader than Type-2 and can be made nondegenerate by temperature tuning. In addition, the authors reported that the pair generation (per nm) of type-0 is about 10 times higher than that of type-2.

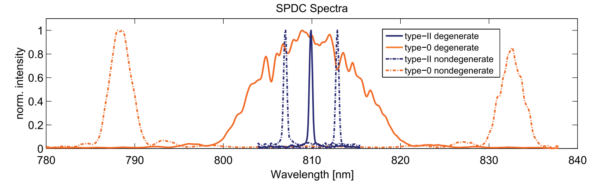
To make things a little more complicated, the dispersion and the length of the KTP Crystal also affects the spectral bandwidth and pair rate. Longer crystals generate more pairs at the cost of reduced spectral bandwidth, and signal/idler photons are much broader at telecom wavelengths (~1550) than they are at NIR (~810).

All these examples show that PPKTP is an extremely versatile component, and it is therefore important to first consider the needs of each application before choosing the right crystal. Below we present a few recent utilizations of PPKTP for various applications and provide our recommended crystal. We are proud to say that all this knowledge came from the brilliant researchers that use our PPKTP Crystals and shared their findings with the scientific community. Feel free to contact us if you think we are missing a key application or research work.

Boson Sampling and quantum interference

In Boson Sampling, quantum light is usually placed at the input of a large interferometer that includes multiple splitting and re-combining of beams. Boson Sampling relies on quantum interference (Hong-Ou-Mandel effect) and therefore benefits from high spectral purity. Special efforts were made by the Fedrizzi group for creating aperiodically polled crystals for high spectral purity at 1550nm [2], and a similar design was implemented by USTC’s photonic quantum supremacy experiment [3]. Recent quantum computing efforts by Xanadu [4] and QuiX [5] utilized PPKTP at the same wavelength region, due to both higher purity at these wavelengths and compatibility with peripheral platforms such as Silicon Nitride. Raicol has developed (through a collaboration with Prof. Ady Arie) a method for the design and manufacture of high spectral purity APKTP Crystals for Boson sampling and quantum interference close to the group velocity matching point of 1550nm.

Recommended Crystal: Type-2 APKTP or PPKTP at 775->1550. APKTP offers higher spectral purity while PPKTP offers higher pair rate.

Quantum Key Distribution

PPKTP plays a role in entanglement-based QKD as a source of polarization-entangled photon pairs. In this field there are many available options depending on whether the system is designed for free-space or fiber. In general, detector efficiency and the availability of 405nm lasers usually pushes these applications towards entanglement at 810nm [6, 7]. Type-2 crystals are easier to use because of their narrow linewidth, easy separation of the signal and idler with a polarizing beam splitter, and robustness to temperature, while type-0 crystals are broader and offer higher pair rate, making them good candidates for multiplexed QKD [8].

Recommended Crystal: Type-0 or Type-2 PPKTP at 405->810. Type-0 offers higher pair rate and spectral bandwidth, while Type-2 offers ease of usability.

Squeezed Light

Squeezed light usually utilizes the crystals in the strong pumping regime (unlike heralded single photons or polarization entanglement), and benefits from a strong nonlinear response, therefore making type-0 crystals the favorable option. Examples include the Furusawa group with 9dB of squeezing at 860nm [9], The Schnabel group has demonstrated 15dB and 13dB of squeezing at both 1064 and 1550nm [10, 11], and the Bowen group using the former for a demonstration of squeezing-enhanced microscopy [12]. Squeezed light can be generated anywhere from 780nm (390nm pump) to 3.8 microns and is a function of the exact specific application.

When choosing a crystal for squeezed light applications, the researcher should first decide if the squeezing is going to be generated in single-pass or in a cavity. For the former, a standard crystal suffices, while for an optimal parametric oscillator, monolithic or hemi-monolithic options are preferred [13].

Recommended Crystal: Type-0 ppKTP, optional hemi or fully monolithic.

Imaging With Undetected Photons

Imaging with undetected photons usually utilizes type-0 crystals with varying degeneracy. For fundamental research it is convenient to be able to detect both photons [14], while the Ramelow group generated a signal in the visible and idler at the mid-IR for microscopy applications [15].

Recommended Crystal: Type-0 PPKTP, with a period that is designed for nondegeneracy. No better example than Ramelow’s 660->800+3800.

We will try to update this list periodically, so visit this page every now and then!

Bibliography

[1] Steinlechner et al. “Efficient heralding of polarization-entangled photons from type-0 and type-II spontaneous parametric downconversion in periodically poled KTiOPO4”, JOSA B 31, 9, 2068-2076 (2014).

[2] Graffitti et al. “Independent high-purity photons created in domain-engineered crystals”, Optica 5, 5, 514-517 (2018).

[3] Zhong et al. “Quantum computational advantage using photons”, Science 370, 6523, 1460-1463 (2020).

[4] Madsen et al. “Quantum computational advantage with a programmable photonic processor”, Nature 606, 75–81 (2022).

[5] Taballione et al. “20-Mode Universal Quantum Photonic Processor”, arXiv:2203.01801.

[6] Yin et al. “Entanglement-based secure quantum cryptography over 1,120 kilometres”, Nature 582, 501–505 (2020).

[7] Mishra et al. “BBM92 quantum key distribution over a free space dusty channel of 200 meters”, Journal of Optics, 24, 7 (2022).

[8] Brambila et al. “Ultrabright Polarization-Entangled Photon Pair Source for Frequency-Multiplexed Quantum Communication in Free-Space”, arXiv:2205.10214.

[9] Takeno et al. “Observation of -9 dB quadrature squeezing with improvement of phase stability in homodyne measurement”, Optics Express 15, 7, 4321-4327 (2007).

[10] Vahlbruch et al. “Detection of 15 dB Squeezed States of Light and their Application for the Absolute Calibration of Photoelectric Quantum Efficiency”, Physical Review Letters 117, 110801 (2016).

[11] Schönbeck et al. “13 dB squeezed vacuum states at 1550 nm from 12 mW external pump power at 775 nm”, Optics Letters 43, 1, 110-113 (2018).

[12] Casacio et al. “Quantum-enhanced nonlinear microscopy”, Nature 594, 201–206 (2021).

[13] Ast et al. “High-bandwidth squeezed light at 1550 nm from a compact monolithic PPKTP cavity”, Optics Express 21, 11, 13572-13579 (2013).

[14] Gilaberte Basset et al. “Video-Rate Imaging with Undetected Photons”, Laser & Photonics Reviews 15, 6 (2021).

[15] Kviatkovsky et al. “Microscopy with undetected photons in the mid-infrared”, Science Advances 6, 42 (2020).

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Dr. Noa Voloch Bloch and Ori Levin

Difference Frequency Generation (DFG) and Sum Frequency Generation (SFG) are crucial processes in modern laser systems, allowing for the generation of new optical frequencies by mixing two distinct wavelengths. For professionals in industries such as defense, aerospace, medical, and industrial applications, selecting the right nonlinear crystal is critical to achieving optimal performance.

With over 50 years of experience in crystal growth, Raicol Crystals is at the forefront of providing high-quality nonlinear optical crystals and electro-optical components for laser systems worldwide. In this article, we will explore key aspects of DFG and SFG and how Raicol’s expertise in crystal manufacturing can significantly enhance the efficiency and precision of your laser systems.

1. What are Difference Frequency Generation (DFG) and Sum Frequency Generation (SFG) and How Do They Work? Difference Frequency Generation (DFG) is a nonlinear optical process in which two laser beams with different frequencies mix within a nonlinear crystal to produce a new output beam at the frequency difference between the two input beams. Conversely, Sum Frequency Generation (SFG) combines two input wavelengths to create a new beam at the sum of their frequencies. The crystals’ nonlinear susceptibility couples between the different laser input and create a new frequency output.

2. These techniques are essential for producing tunable sources of coherent radiation in the infrared, terahertz, and visible regions.

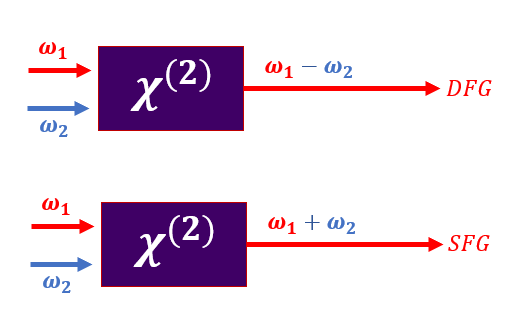
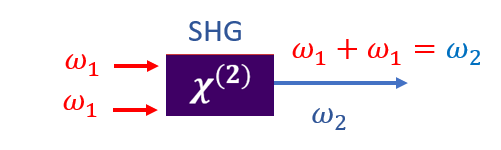
Second Harmonic Generation (SHG) is a special case of Sum Frequency Generation (SFG) where two photons of the same frequency combine to produce a single photon with twice the frequency (or half the wavelength) of the input light. In this degenerate process, two identical photons from the fundamental beam are converted into one photon at the second harmonic through interaction with a nonlinear optical material.

The efficiency of this process depends critically on phase-matching conditions within the nonlinear crystal. SHG has become a widely used technique for generating new frequencies, particularly for accessing shorter wavelengths in laser systems and spectroscopic applications.

Raicol Crystals specializes in providing nonlinear crystals optimized for both DFG and SFG applications. By selecting the right material and engineering the crystal to meet specific wavelength requirements, Raicol ensures that DFG and SFG systems achieve high efficiency, precision, and stability. This makes their nonlinear crystals ideal for advanced laser systems requiring reliable and precise frequency control.

2. Which Nonlinear Crystals are Suitable for DFG and SFG?

The efficiency of DFG and SFG processes depends significantly on the nonlinear crystal’s properties, including its nonlinear coefficient, damage threshold, and phase-matching capabilities. Commonly used nonlinear crystals for DFG and SFG include Potassium Titanyl Phosphate (KTP), Beta Barium Borate (BBO), and periodically poled lithium niobate (PPLN). These materials offer excellent nonlinear properties, high damage thresholds, and thermal stability in various wavelength ranges.

Raicol Crystals specializes in high-quality oxide-based nonlinear crystals, such as these, that are designed to handle high power, high efficiency, and thermal stability in laser systems. Additionally, Raicol’s ability to offer customized solutions means that customers can select the optimal material tailored to their specific DFG and SFG needs. Whether it’s for medical diagnostics, industrial applications, or defense systems, Raicol’s products ensure maximum performance in frequency generation applications.

3. How do Nonlinear Crystals Enhance DFG and SFG Efficiency?

The efficiency of DFG and SFG heavily relies on the properties of the nonlinear crystal, such as its nonlinear coefficient, transparency range, and phase-matching capabilities. For maximum efficiency, the crystal must support the specific phase-matching conditions for the wavelengths of the input beams.

Raicol Crystals leverages over 50 years of expertise in crystal growth to provide customized solutions that enhance DFG and SFG efficiency. Their nonlinear crystals are optimized for high conversion efficiency, low losses, and the ability to handle high-power lasers. Raicol’s advanced manufacturing processes ensure that each crystal is precisely engineered to support the phase-matching conditions, allowing for superior performance in demanding applications.

Raicol’s tailored solutions enable clients to achieve the best possible output from their DFG and SFG systems, improving efficiency and ensuring reliable, high-quality results, particularly in critical industries like defense, aerospace, and medical diagnostics.

4. Why Choose Raicol Crystals for DFG and SFG Applications in Industrial and Defense Sectors?

Raicol Crystals is a global leader in manufacturing nonlinear crystals, with deep expertise in the specific requirements of the defense and industrial sectors. Their advanced crystal solutions enable high-performance systems essential for applications like advanced radar, laser weapons, and high-resolution spectroscopy.

By offering customized nonlinear crystals that are engineered to meet the specific needs of these industries, Raicol ensures that its customers can achieve the precision and reliability required for mission-critical systems. Whether you’re designing next-generation defense technologies or enhancing industrial laser applications, Raicol’s nonlinear crystals provide the high performance necessary for success.

5. How Raicol Crystals Supports Medical Field with DFG and SFG Applications?

In the medical field, DFG and SFG processes are used in non-invasive imaging techniques. The ability to generate precise wavelengths through these frequency generation methods enables improved resolution and sensitivity in medical imaging systems, making them valuable tools for diagnostics.

Raicol Crystals manufactures nonlinear optical crystals that are ideal for DFG and SFG applications in medical imaging. Their customized crystals ensure high frequency conversion efficiency, enhancing the performance of optical diagnostic devices. By optimizing the wavelength conversion process, Raicol’s crystals improve the clarity and accuracy of medical images, aiding in better diagnostic procedures and patient outcomes.

Conclusion: Why Raicol Crystals is the Optimal Choice for DFG and SFG Applications Difference Frequency Generation (DFG) and Sum Frequency Generation (SFG) play critical roles in many of today’s advanced optical technologies. For industries like defense, aerospace, medical, and industrial applications, the performance of DFG and SFG systems is intrinsically linked to the quality of the nonlinear crystals used.

Raicol Crystals, with over 50 years of expertise in crystal growth and a proven track record of providing high-quality nonlinear optical crystals, is the ideal partner for your DFG and SFG applications. Their commitment to precision, customized solutions, and high-performance products ensures that your frequency generation systems operate at peak efficiency and deliver optimal results.

Whether you’re enhancing the performance of existing laser systems or developing cutting-edge technologies, Raicol Crystals provides the knowledge, technology, and products needed to succeed.

Explore Raicol’s range of nonlinear optical crystals and electro-optical components to take your DFG \SFG systems to the next level.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Frequency Conversion

Electro optics modules

Quantum Components

Our Catalog

Electro-Optic Modulators: RTP vs. BBO Architectures

1. The Acoustic Ringing Barrier in MHz Cavities

2. RTP & BBO Electro-Optic Specification Comparison

RTP Pockels Cell Specifications

BBO Pockels Cell Specifications

3. Advanced Electro-Optic Manufacturing & Assembly

4. Design Considerations in Electro-Optic Cavities

5. Engineering Consultation

Crystal Selection for Difference Frequency Generation

1. Why DFG for the Mid-Infrared

2. Quasi-Phase Matching versus Birefringent Phase Matching

3. Selecting a QPM Crystal for Mid-IR DFG

4. QPM Specification Comparison

5. High Average Power: Where HGTR KTP Belongs

6. Advanced Poling Architectures

7. Design Considerations in DFG Cavities

8. Engineering Consultation

From rings and crossed crystals to interferometers

Let the poling do the heavy lifting

The Quantum Hallmark: Correlations in Multiple Bases

Certifying High-Dimensional Entanglement with SFG

The Crystal Connection

Electro-Optic Devices for High-Speed Laser Control

RTP EO Cells and Pockels Cells

iRTP Pockels Cells

Applications for EO Devices

Crystal-Based Frequency Conversion Solutions

Quantum Applications - PPKTP and Beyond

Raicol is developing advanced solutions for integrated photonics:

The Crystal Choice: Operating Temperature and Intrinsic Noise

Raicol: Precision Crystals for Quantum Light

The Power of Monolithic Cavities

Record Low Noise and Quantum State Preservation

The Path Forward

Classical Dispersion: The Spreading of Light

Franson’s Nonlocal Dispersion Cancellation

Steinberg’s Local Dispersion Cancellation

Developments Since the 1990s

Implications and Applications

Quantum and classical ghost imaging

Computational ghost imaging

Current state and future directions

Boson Sampling and quantum interference

Quantum Key Distribution

Squeezed Light

Imaging With Undetected Photons

Bibliography

2. Which Nonlinear Crystals are Suitable for DFG and SFG?

3. How do Nonlinear Crystals Enhance DFG and SFG Efficiency?

4. Why Choose Raicol Crystals for DFG and SFG Applications in Industrial and Defense Sectors?

5. How Raicol Crystals Supports Medical Field with DFG and SFG Applications?

Download Catalog

Download Quantum Catalog