Author: Ronen Shekel
Imagine a box with two balls: one red, one blue. Alice takes one ball to Mars and Bob takes the other to Andromeda. The moment Alice opens her box and sees a blue ball: she instantly knows Bob’s is red. This might seem like what Einstein called “spooky action at a distance” [1], but it is not entanglement. This is classical correlation. The properties were fixed from the start.
The Quantum Hallmark: Correlations in Multiple Bases
A hallmark of quantum entanglement is the existence of strong correlations in multiple, incompatible measurement bases [2].
Consider a Bell state, a state in a coherent superposition of horizontal and vertical polarizations, |HH>+|VV>. If Alice and Bob both agree to measure in the H/V basis (for example, by setting their polarizers to 0°/90°), they will find perfect correlations: if Alice gets H, Bob gets H. If she gets V, he gets V. So far, this is just like the red and blue balls.
But if they both agree to switch to an incompatible basis, like the basis of diagonal (D) and anti-diagonal (A) polarization, their results will still be perfectly correlated. This is unique to coherent quantum correlations.
Now, compare this to a simple, non-entangled state, like |HH>. In the H/V basis, their results are perfectly correlated. But if they both measure in the D/A basis, the correlations vanish. The results are random; if Alice measures D, she has no idea if Bob will get D or A.
Bell inequalities are tests designed to measure these very correlations across multiple bases [3, 4]. Rigorous certification of entanglement by violating these inequalities is essential for quantum technologies, from quantum computing to secure communication.
Certifying High-Dimensional Entanglement with SFG
This concept isn’t limited to two-dimensional polarization. As we’ve discussed in a previous post on spatial entanglement, entanglement can be high-dimensional, existing in the spatial properties of photons, where two mutually unbiased bases could be for instance the near-field and far-field distributions. Entanglement could also manifest in the time-energy properties of photon pairs.
In Spontaneous Parametric Down-Conversion (SPDC), a narrowband pump photon splits into two twin photons. Due to energy conservation, the sum of their frequencies ν₁ + ν₂ is precisely fixed. And because they are born at the same instant, the time difference between them (t₁ − t₂) is incredibly small.
For any separable, classical-like state, the uncertainties in these correlated quantities obey a fundamental bound: Δ(t₁ − t₂)Δ(ν₁ + ν₂) ≥ 1⁄2 [5]. A quantum-entangled pair, however, can violate this.
To prove this violation, we cannot simply measure the individual times and frequencies of each photon separately, since doing so would destroy the joint correlation information we seek to certify. Instead, we must perform a global measurement that probes the combined variables (t₁ − t₂) and (ν₁ + ν₂) directly, without accessing the individual values.
Sum-Frequency Generation (SFG) is an ideal tool for this. As the reverse of SPDC (Fig. 1), SFG requires both photons to arrive simultaneously at the crystal, effectively acting as an ultrafast coincidence detector for t₁ − t₂ ≈ 0. Furthermore, it annihilates both photons to create one new photon whose frequency is the sum ν₁ + ν₂, which can then be measured precisely.
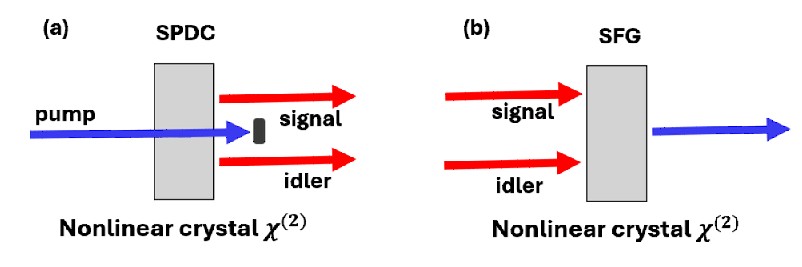
While this idea has been known for years [6, 7], direct SFG with single photons is notoriously inefficient. Recently [8], a groundbreaking experiment from Prof. Avi Pe’er’s group at Bar-Ilan University shattered this barrier, violating the classical bound by an astonishing 12 orders of magnitude. Using a high-quality PPKTP crystal to generate biphotons with an extreme bandwidth of 113 THz, they employed Coherent SFG, where a strong pump stimulates the recombination, to efficiently and directly measure the joint correlation.
The Crystal Connection
The success of such record-breaking work relies on the exceptional quality of nonlinear crystals. At Raicol we are proud to provide such high-quality crystals and are happy to contribute to research pushing the boundaries of quantum science. We are also active participants in international collaborations, such as the European QuantERA project SPARQL, dedicated to advancing quantum technologies.
Time-energy entanglement arises naturally and intrinsically in SPDC through energy conservation – it requires no additional engineering. But how can we engineer entanglement in the polarization degree of freedom? Stay tuned for our next post.
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
References
[1] Einstein, A., & Born, M. (1971). Letter from Einstein to Max Born, 3 March 1947. In B. M. Walker (Ed.), The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955 (pp. 157-158). New York.
[2] Giese, Enno. “Entanglement and Its Verification: A Tutorial on Classical and Quantum Correlations.” arXiv preprint arXiv:2511.09507 (2025).
[3] Bell, John S. “On the einstein podolsky rosen paradox.” Physics Physique Fizika 1, no. 3 (1964): 195.
[4] Clauser, John F., Michael A. Horne, Abner Shimony, and Richard A. Holt. “Proposed experiment to test local hidden-variable theories.” Physical review letters 23, no. 15 (1969): 880.
[5] Mei, Yefeng, Yiru Zhou, Shanchao Zhang, Jianfeng Li, Kaiyu Liao, Hui Yan, Shi-Liang Zhu, and Shengwang Du. “Einstein-podolsky-rosen energy-time entanglement of narrow-band biphotons.” Physical Review Letters 124, no. 1 (2020): 010509.
[6] Dayan, Barak, Avi Pe’er, Asher A. Friesem, and Yaron Silberberg. “Nonlinear interactions with an ultrahigh flux of broadband entangled photons.” Physical review letters 94, no. 4 (2005): 043602.
[7] MacLean, Jean-Philippe W., John M. Donohue, and Kevin J. Resch. “Direct characterization of ultrafast energy-time entangled photon pairs.” Physical review letters 120, no. 5 (2018): 053601.
[8] Nechushtan, Nir, Hanzhong Zhang, Yosef London, Mallachi Meller, Haia Amichai, Eliahu Cohen, and Avi Pe’er. “Quantum matched filtering: breaking time-energy separability by 12 orders of magnitude.” arXiv preprint arXiv:2503.03583 (2025).
In modern quantum optics and integrated photonics, precise control over light is essential. Laboratories and industrial applications require devices that offer high speed, stability, and reproducibility. Raicol has established itself as a leading provider of electro-optic devices and nonlinear crystal systems, offering products that enable precise laser modulation, pulse shaping, and frequency conversion for demanding scientific environments. Raicol’s portfolio includes Pockels cells, phase and amplitude modulators, Q-switches, pulse pickers, and a range of advanced nonlinear systems for second harmonic generation (SHG), third harmonic generation (THG), optical parametric oscillation (OPO), and spontaneous parametric down-conversion (SPDC) processes.
Electro-Optic Devices for High-Speed Laser Control
Electro-optic (EO)devices leverage the Pockels effect in nonlinear crystals to modulate laser beams at high speed with nanosecond precision. These devices are central to modern photonics research, enabling scientists to control polarization, phase, and amplitude with exceptional accuracy.
RTP EO Cells and Pockels Cells
Raicol’s RTP (Rubidium Titanyl Phosphate) EO cells are the foundation of their electro-optic product line. RTP belongs to the KTP crystal family and offers outstanding electro-optical properties:
- Ultra-fast response: Rise time, fall time, and pulse width < 1 ns
- High damage threshold: Over 1 GW/cm² at 1064 nm (typical >2 GW/cm²)
- Wide temperature stability: Operating range from -50°C to 70°C
- Non-hygroscopic: Easy handling, no protective cover needed
- High extinction ratio: >35 dB
- Low half-wave voltage: Enables compact design
- Minimal acoustic ringing: Compatible for over 1 MHz repetition rate

iRTP Pockels Cells
Raicol’s iRTP (industrial RTP) brings the advantages of RTP to the mass market:
- Industrial price point: Standard off-the-shelf solution at competitive pricing
- Simplified alignment: Requires only 1-axis alignment vs. 3-axis for KD*P
- Thermal stability: 10°C to 50°C operational range without thermal control
- High damage threshold: Typically > 1 GW/cm²
- Fast response: <1 ns rise time
- No acoustic ringing: Up to at least 350 kHz
Applications for EO Devices
- Q-Switches: For generating high-energy, short-duration laser pulses
- Pulse Pickers: Enabling selection of individual pulses from high-repetition-rate laser trains
- Phase Modulators: For precise manipulation of optical phase
- Amplitude Modulators: For controlled laser attenuation and modulation
- Cavity Dumpers: For extracting stored energy from laser cavities
- Optical Shutters: For precise laser beam gating
- Attenuators & Deflectors: For beam control applications
Crystal-Based Frequency Conversion Solutions
Raicol offers a comprehensive suite of nonlinear crystal solutions for wavelength conversion, essential for many advanced laser applications.
Second Harmonic Generation (SHG) Crystals
KTP Crystals: The most common nonlinear crystal for SHG of YAG lasers
- SHG coefficient approximately three times higher than KDP
- High laser damage threshold: 1 GW/cm² at 1064 nm
- Large aperture capability: up to 50×50 mm
- Excellent thermal stability
HGTR (High Gray Track Resistance) KTP: For high-power applications
- Average output power density at 532 nm up to 5 kW/cm²
- Nonlinear coefficient 4 times higher than LBO
- Designed to resist gray track formation at high power
LBO (Lithium Triborate) Crystals:
- Super polished surface quality: roughness ≤ 3Å RMS
- Very low bulk absorption: up to 2 ppm/cm at 1064 nm
- High damage threshold: 2500 MW/cm² at 1064 nm
- Wide transparency range: 160-2600 nm
Third Harmonic Generation (THG)
CLBO (Caesium Lithium Borate): Ideal for deep UV applications
- Wide transmission range: 180-2750 nm
- Enables frequency conversion below 200 nm
- Applications: 4th and 5th harmonics of Nd:YAG, 7th and 8th harmonics of 1550 nm
Optical Parametric Oscillation (OPO)
KTP OPO Crystals: Most efficient for converting 1064 nm to 1572 nm (“eye safe”)
- Non-critical phase matching (NCPM) for 1572 nm with no walk-off
- Available in monolithic configurations with 20-30% higher efficiency
- Apertures up to 40×40 mm, lengths up to 40 mm
Quantum Applications - PPKTP and Beyond
PPKTP (Periodically Poled KTP): Raicol pioneered this technology over 20 years ago
- Quasi-phase matching (QPM) enables efficient SPDC processes
- Three times larger effective nonlinear coefficient than bulk KTP
- Type-0 or Type-II phase matching options
- Broad pumping range: 405 nm, 532 nm, 775 nm
HP-APKTP (High Purity Aperiodically Poled KTP):
- Aperiodic poling shapes the joint spectrum of SPDC
- Higher spectral purity without external filters
- Improved Hong-Ou-Mandel visibility compared to standard ppKTP
- Type-2 crystal suitable for Ti-Sapphire laser pumping (775-795 nm)
PPKTP Innovations:
- Waveguides: 23× higher nonlinear efficiency compared to bulk crystals
- Monolithic crystals: Mirror-coated facets for squeezed light generation
- 2D poling: For spatial qudit generation and quantum holography
- Short poling periods: Down to 1.2 μm for narrow-band counter-propagation SPDC
Integrated Photonics and Future Technologies
Raicol is developing advanced solutions for integrated photonics:
Waveguide Technologies
- ppKTP waveguides: Enhanced pair generation efficiency (>10× bulk efficiency)
- RTP waveguide modulators: For integrated photonic applications
- Thin film RTP: Optimized for silicon photonics integration
Quantum Components
- Heralded Single-Photon Modules: Fiber-coupled, integrated with thermal control
- Entangled Photon Sources: Sagnac-loop design with >95% visibility
- Squeezed Light Sources: Monolithic ppKTP for quantum sensing
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
Medical imaging relentlessly pushes toward higher resolution. Distinguishing features separated by mere micrometers can mean the difference between early disease detection and a missed diagnosis. However, conventional optical coherence tomography (OCT), despite impressive resolution, faces a fundamental tradeoff: as bandwidth broadens to enhance resolution, dispersion in biological tissues increasingly smears the very features we seek to resolve.
Quantum optics offers a remarkable solution. By harnessing entangled photon pairs from specially engineered crystals, we can completely cancel the effect of sample dispersion and achieve twice the axial resolution of classical methods. The key enabler is chirped aperiodically poled KTP (APKTP), which generates the ultra-broadband entangled photons essential for this quantum sensing achievement.
Broadband biphoton generation
High temporal resolution requires a broad frequency spectrum – a fundamental Fourier relationship. For quantum technologies using photon pairs, this means generating photons entangled over vast frequency ranges.
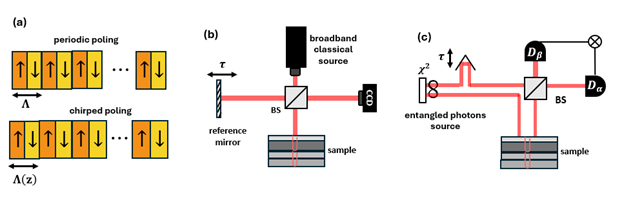
Standard periodically poled crystals (PPKTP) phase match only relatively narrow frequency bands. Chirped APKTP, however, gradually varies the poling period along the crystal length (Fig. 1a), phase-matching different frequencies at distinct positions along the crystal [1-3]. This seamlessly integrates multiple phase-matching conditions into a single crystal, enabling photon pairs to span ultrabroad spectra. Such chirped crystals have demonstrated a bandwidth of 300nm, with record-breaking Hong-Ou-Mandel (HOM) interference of <10 fs width [1], a hallmark of ultrashort temporal correlations [4]. This spectral engineering is invaluable also for advanced quantum imaging [5], spectroscopy [6] and tomography [7] applications.
A different method for broadband biphoton generation is utilizing a natural advantage of KTP: it has a zero group-velocity dispersion wavelength at approximately 1789 nm for light polarized along the crystallographic Z axis of KTP [8,9]. Near this “sweet spot,” the bandwidth of type-0 SPDC is limited only by higher-order dispersion, enabling biphoton spectral widths approaching 1000 nm even without chirped poling.
Classical and quantum OCT
Optical coherence tomography uses broadband light in a low-coherence interferometer to create cross-sectional images of subsurface structures. Light split between reference and sample arms (Fig. 1b) produces interference only when path lengths match within the source’s coherence length, enabling depth profiling with a precision resolution of a few μm in medical applications.
However, OCT faces a practical limitation: group velocity dispersion. Different wavelengths travel at different speeds through materials, smearing pulses and reducing resolution. Consequently, as bandwidth broadens to improve resolution, dispersion increasingly limits OCT’s performance.
Quantum Optical Coherence Tomography (QOCT), proposed in 2002 [10,11], utilizes spectrally entangled photon pairs where one photon probes the sample while its twin serves as a reference (Fig. 1c). This quantum approach provides two remarkable advantages. First, it inherently cancels sample dispersion effects through a local dispersion cancellation effect [12], which we discussed in a previous post. Second, QOCT delivers a factor-of-two improvement in axial resolution: Two-photon quantum interference depends on the paths travelled by both photons, doubling sensitivity to optical delays compared to classical methods.
Since 2002 many advancements have been made in the field of classical OCT, with new ideas such as spectral-domain OCT and swept-source OCT [13], as well as new quantum OCT configurations [7].
Combining LBO optical parametric amplifier with CPA – (OPCPA).
Over the last decade domain engineering has undergone significant development [14], and here at Raicol, we advance the available technology by producing advanced crystals like chirped APKTP to translate quantum concepts into reality. Our expertise in periodic and aperiodic poling allows custom crystals optimized for various quantum applications. Through collaborations like the European QuantERA project SPARQL, we’re committed to advancing quantum technologies. Contact us to discuss how our crystal engineering can empower your quantum research and products.
References
[1] Nasr, Magued B., Silvia Carrasco, Bahaa EA Saleh, Alexander V. Sergienko, Malvin C. Teich, Juan P. Torres, Lluis Torner, David S. Hum, and Martin M. Fejer. “Ultrabroadband biphotons generated via chirped quasi-phase-matched optical parametric down-conversion.” Physical review letters 100, no. 18 (2008): 183601.
[2] Brida, Giorgio, M. V. Chekhova, I. P. Degiovanni, M. Genovese, G. Kh Kitaeva, A. Meda, and O. A. Shumilkina. “Chirped biphotons and their compression in optical fibers.” Physical review letters 103, no. 19 (2009): 193602.
[3] Wang, Jinbao, and Haibo Lin. “The single-cycle biphotons generated by noncollinear SPDC in the chirped QPM crystals.” Journal of the European Optical Society-Rapid Publications 20, no. 1 (2024): 6.
[4] Hong, Chong-Ki, Zhe-Yu Ou, and Leonard Mandel. “Measurement of subpicosecond time intervals between two photons by interference.” Physical review letters 59, no. 18 (1987): 2044.
[5] Lemos, Gabriela Barreto, Victoria Borish, Garrett D. Cole, Sven Ramelow, Radek Lapkiewicz, and Anton Zeilinger. “Quantum imaging with undetected photons.” Nature 512, no. 7515 (2014): 409-412.
[6] Kalashnikov, Dmitry A., Anna V. Paterova, Sergei P. Kulik, and Leonid A. Krivitsky. “Infrared spectroscopy with visible light.” Nature Photonics 10, no. 2 (2016): 98-101.
[7] Vanselow, Aron, Paul Kaufmann, Ivan Zorin, Bettina Heise, Helen M. Chrzanowski, and Sven Ramelow. “Frequency-domain optical coherence tomography with undetected mid-infrared photons.” Optica 7, no. 12 (2020): 1729-1736.
[8] Viotti, Anne-Lise. Nonlinear optics in KTiOPO4 for spectral management of ultra-short pulses in the near-and mid-IR. Diss. KTH Royal Institute of Technology, 2019.
[9] https://refractiveindex.info
[10] Abouraddy, Ayman F., Magued B. Nasr, Bahaa EA Saleh, Alexander V. Sergienko, and Malvin C. Teich. “Quantum-optical coherence tomography with dispersion cancellation.” Physical Review A 65, no. 5 (2002): 053817.
[11] Nasr, Magued B., Bahaa EA Saleh, Alexander V. Sergienko, and Malvin C. Teich. “Demonstration of dispersion-canceled quantum-optical coherence tomography.” Physical review letters 91, no. 8 (2003): 083601.
[12] Steinberg, Aephraim M., Paul G. Kwiat, and Raymond Y. Chiao. “Dispersion cancellation and high-resolution time measurements in a fourth-order optical interferometer.” Physical Review A 45, no. 9 (1992): 6659.
[13] Ge, Xin, Shufen Chen, Si Chen, and Linbo Liu. “High resolution optical coherence tomography.” Journal of Lightwave Technology 39, no. 12 (2021): 3824-3835.
[14] Weiss, Tim F., and Alberto Peruzzo. “Nonlinear domain engineering for quantum technologies.” Applied Physics Reviews 12, no. 1 (2025).
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
Even the most stable laser isn’t perfectly quiet. The fact that light comes in discrete photons introduces statistical fluctuations known as shot noise, leading to the standard quantum limit for optical measurement precision.
However, quantum optics provides a workaround. A squeezed state redistributes uncertainty, shrinking noise in one property (phase or amplitude) below the shot‑noise floor while increasing it in the other. On a phase-amplitude diagram the round noise circle turns into an elongated ellipse. Such engineered low-noise light boosts the sensitivity of LIGO’s gravitational‑wave detectors [1], squeezed‑light magnetometers [2], and many other quantum sensing and communication applications.
A common method to generate squeezed light is through a Degenerate Optical Parametric Amplifier (DOPA). In a DOPA, a strong pump laser beam interacts with a nonlinear crystal, typically placed inside an optical cavity to enhance the interaction, and drives the generation of photon pairs. The phase‑sensitive nature of the process allows the cavity to reduce fluctuations along one quadrature while amplifying the orthogonal one. The strength of this interaction is characterized by its effective nonlinear coefficient; a higher value usually indicates a more efficient conversion process, which can translate to stronger squeezing for a given crystal length and pump power.
The Crystal Choice: Operating Temperature and Intrinsic Noise
Two prominent nonlinear materials for constructing DOPAs are periodically poled Potassium Titanyl Phosphate (PPKTP) and periodically poled Lithium Niobate (PPLN). PPLN has a higher nonlinear coefficient than PPKTP, suggesting it is inherently better for generating strong squeezing. However, practical operational requirements introduce crucial differences.
PPLN often suffers from a photorefractive effect when exposed to high-intensity laser light near room temperature. This effect involves the light-induced generation and migration of charge carriers within the crystal, creating internal electric fields that distort the crystal’s refractive index and degrade the quality of the transmitted laser beams. To mitigate photorefraction, PPLN-based devices are typically operated at high temperatures, such that the trapped charges have enough energy to become mobile again, averaging out the internal fields and mitigating the effect. In contrast, PPKTP-based DOPAs can operate efficiently near room temperature without significant photorefractive problems.
This difference in operating temperature has significant consequences for the ultimate noise performance. At elevated temperatures, the atomic lattice vibrates, resulting in microscopic acoustic waves propagating through the crystal. These waves randomly modulate the refractive index. This phenomenon, known as Guided Acoustic Wave Brillouin Scattering (GAWBS), introduces a fundamental source of phase noise that is directly dependent on the crystal’s temperature [3].
A direct experimental comparison by Wan et al. highlighted this critical trade-off [4]. Using identical 1550 nm DOPA setups, they found 6.8 dB of squeezing – that is, 6.8 dB of noise reduction below the standard quantum limit – for room-temperature PPKTP versus 4.9 dB using PPLN at 135°C. The superior squeezing performance of PPKTP, despite its lower nonlinear coefficient, was directly attributed to the reduced GAWBS-induced phase noise at its cooler operating temperature.
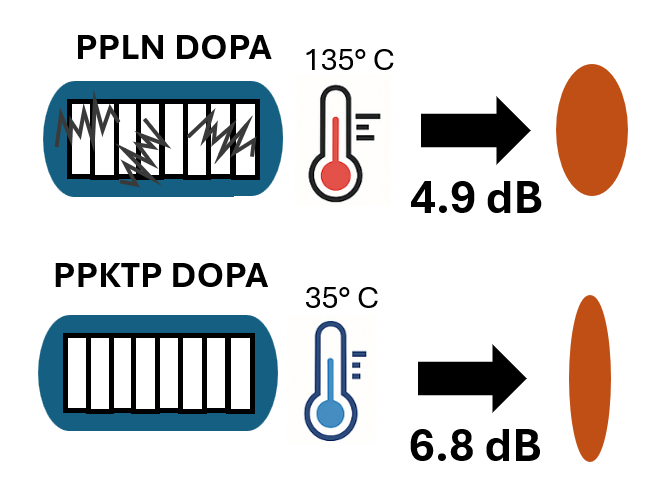
For the strongest phase squeezing, eliminating GAWBS matters more than the absolute value of the nonlinear coefficient. Indeed, record squeezing levels of 12 dB at 1550 nm and 15 dB at 1064 nm both used PPKTP [5, 6], underlining its exceptional low-noise properties.
Raicol: Precision Crystals for Quantum Light
Deep squeezing requires crystals with precisely controlled poling, ultralow absorption, and exceptional uniformity. Raicol’s PPKTP crystals are engineered to these exacting standards, with options for custom periodicities and aperiodic poling designs. For your next squeezed light source, we invite you to explore our products and consult with our team to identify the optimal crystal configuration for your specific applications.
References
[1] Aasi, Junaid, Joan Abadie, B. P. Abbott, Richard Abbott, T. D. Abbott, M. R. Abernathy, Carl Adams et al. “Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light.” Nature Photonics 7, no. 8 (2013): 613-619.
[2] Wolfgramm, Florian, Alessandro Cere, Federica A. Beduini, Ana Predojević, Marco Koschorreck, and Morgan W. Mitchell. “Squeezed-light optical magnetometry.” Physical review letters 105, no. 5 (2010): 053601.
[3] César, Jônatas Eduardo da Silva, A. S. Coelho, Katiuscia Nadyne Cassemiro, Alessandro de Sousa Villar, M. Lassen, P. Nussenzveig, and Marcelo Martinelli. “Extra phase noise from thermal fluctuations in nonlinear optical crystals.” Physical Review A—Atomic, Molecular, and Optical Physics 79, no. 6 (2009): 063816.
[4] Wan, Zhenju, Jinxia Feng, Yuanji Li, and Kuanshou Zhang. “Comparison of phase quadrature squeezed states generated from degenerate optical parametric amplifiers using PPKTP and PPLN.” Optics express 26, no. 5 (2018): 5531-5540.
[5] Mehmet, Moritz, Stefan Ast, Tobias Eberle, Sebastian Steinlechner, Henning Vahlbruch, and Roman Schnabel. “Squeezed light at 1550 nm with a quantum noise reduction of 12.3 dB.” Optics express 19, no. 25 (2011): 25763-25772.
[6] Vahlbruch, Henning, Moritz Mehmet, Karsten Danzmann, and Roman Schnabel. “Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency.” Physical review letters 117, no. 11 (2016): 110801.
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
Building large-scale quantum networks hinges on connecting different quantum systems, but these often operate at distinct optical wavelengths. Nitrogen-vacancy centers in diamond, for instance, are excellent candidates for quantum network nodes, emitting single photons at 637 nm [1].
However, transmitting these photons efficiently over long distances through standard optical fibers is problematic, as 637 nm light suffers significant loss. Conversion to the low-loss telecommunication bands is therefore essential.
Quantum frequency conversion (QFC) provides the solution, coherently shifting the wavelength of quantum light while preserving its crucial quantum properties, like entanglement or squeezing. Despite progress, achieving efficient QFC without introducing significant noise has remained a major challenge [2].
Even small amounts of noise can degrade or destroy the fragile quantum states, severely limiting quantum communication and networking capabilities.
A promising new platform, recently demonstrated by Mann et al. [3] using a crystal supplied by Raicol, utilizes a monolithic bulk ppKTP cavity. A “monolithic” cavity means the reflective mirrors forming the optical resonator are coated directly onto the crystal’s end facets, creating a single, integrated device.
This innovative design dramatically boosts the effective power of a modest, off-the-shelf 1064 nm pump laser circulating inside it. The enhanced pump power then efficiently drives the difference frequency generation (DFG) process needed to convert 637 nm photons to the telecom C-band (around 1587 nm in their work), while keeping the generation of unwanted noise photons remarkably low (Fig. 1).
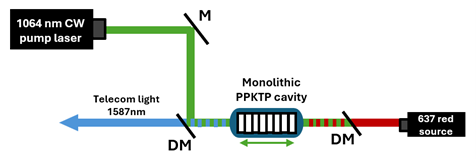
The Power of Monolithic Cavities
Efficient QFC in bulk crystals typically requires high pump powers, often necessitating expensive and complex laser systems. Resonant cavities offer a clever workaround, building up intense light fields inside the crystal from modest input powers. The monolithic design offers specific advantages: it is inherently compact and robust. Furthermore, these cavities can exhibit passive thermal self-tuning [4], meaning they can naturally stay on resonance without needing active electronic feedback loops.
This simplification significantly enhances reliability and practicality for real-world network deployment. Mann et al. [3] also hypothesize that a key advantage comes from using bulk ppKTP: the high quality of periodic poling achievable in bulk KTP [5] may intrinsically suppress parasitic nonlinear processes, particularly unwanted spontaneous parametric down-conversion (SPDC) originating from the strong pump – a major noise source in other QFC approaches.
Record Low Noise and Quantum State Preservation
The Path Forward
The Mann et al. experiment achieved an impressive internal conversion efficiency of up to 72% using only a 3 W input pump laser. Even more significantly, the noise generated was exceptionally low, measured at approximately 110 kHz/nm – a figure quantifying the rate of unwanted noise photons generated per nanometer of bandwidth at the target wavelength. This result represents a 5-fold noise reduction compared to the previous best state-of-the-art single-step converters operating at these wavelengths, dramatically increasing the feasibility of realistic quantum communication links.
Preserving the quantum nature of the light through the conversion process is crucial. The team rigorously verified this by converting single photons from an entangled pair source (SPDC). Measurements of the second-order correlation function confirmed the preservation of non-classical correlations, showing behaviour far exceeding classical limits. They also performed Franson interferometry and a chained Bell inequality test, demonstrating convincingly that time-energy entanglement was preserved with high fidelity through the conversion process.
This work highlights the significant potential of monolithic bulk ppKTP cavities as a robust, efficient, and remarkably low-noise platform for quantum network wavelength conversion. At Raicol Crystals, we provide the high-quality nonlinear crystals essential for this work, including ppKTP, apKTP, and monolithic PPKTP with broadband mirror coatings.
Our expertise in precise periodic and aperiodic poling techniques enables researchers to achieve optimal results in quantum optics applications. We also collaborate with research teams to develop customized monolithic designs that maximize efficiency while maintaining ultra-low noise profiles.
Our ongoing development of narrowband photon sources represents our commitment to advancing quantum technology. Contact Raicol Crystals to explore how our crystals can support your quantum research objectives and help bridge critical wavelength gaps in your experimental systems.
References
[1] Ruf, Maximilian, Noel H. Wan, Hyeongrak Choi, Dirk Englund, and Ronald Hanson. “Quantum networks based on color centers in diamond.” Journal of Applied Physics 130, no. 7 (2021).
[2] Dréau, Anaïs, Anna Tchebotareva, Aboubakr El Mahdaoui, Cristian Bonato, and Ronald Hanson. “Quantum frequency conversion of single photons from a nitrogen-vacancy center in diamond to telecommunication wavelengths.” Physical review applied 9, no. 6 (2018): 064031.
[3] Mann, Felix, Helen M. Chrzanowski, Felipe Gewers, Marlon Placke, and Sven Ramelow. “Low-noise quantum frequency conversion in a monolithic cavity with bulk periodically poled potassium titanyl phosphate.” Physical Review Applied 20, no. 5 (2023): 054010.
[4] Zielińska, Joanna A., and Morgan W. Mitchell. “Self-tuning optical resonator.” Optics letters 42, no. 24 (2017): 5298-5301.
[5] Mann, Felix, Helen M. Chrzanowski, and Sven Ramelow. “Low random duty-cycle errors in periodically poled KTP revealed by sum-frequency generation.” Optics Letters 46, no. 13 (2021): 3049-3052.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
Spontaneous parametric down-conversion (SPDC) is a cornerstone of quantum optics, enabling the generation of entangled photon pairs with remarkable properties. One such property, dispersion cancellation, reveals how entanglement can mitigate effects that typically distort light as it travels through materials. This phenomenon, first explored in the early 1990s, offers both fundamental insights into quantum mechanics and practical applications in quantum technologies. In this post, we discuss how dispersion affects light, how entanglement counters it, and key experiments that have shaped our understanding.
Classical Dispersion: The Spreading of Light
When a short pulse of classical light travels through a vacuum, it retains its compact shape. However, propagation through a material like glass introduces a phenomenon known as dispersion. In a material, the refractive index varies with wavelength, n≈n0+β(λ-λ0 ), where β is the dispersion coefficient at a reference wavelength λ_0, causing different wavelengths of light to travel at different speeds. Since a short pulse comprises a range of wavelengths – owing to its Fourier composition – each component propagates at its own velocity. As a result, the pulse broadens over time.
In materials exhibiting normal dispersion, longer wavelengths (lower frequencies) tend to move faster, while in those with anomalous dispersion, shorter wavelengths (higher frequencies) take the lead. In either case, the outcome is the same: the initially sharp pulse spreads out, losing its compact temporal profile. This effect poses challenges for applications requiring precise timing or short pulses.
Franson’s Nonlocal Dispersion Cancellation
Consider now a pair of spectrally entangled photons generated via SPDC in a nonlinear crystal. A narrowband pump beam splits into two photons – signal and idler – whose frequencies are tightly correlated due to energy conservation (Fig. 1). When measured jointly, their arrival-time correlations are related to the temporal width of their wave-packets, set by their spectral bandwidth via the Fourier transform. But what happens when these photons travel through dispersive media, where dispersion smears each wave-packet and broadens their correlations?
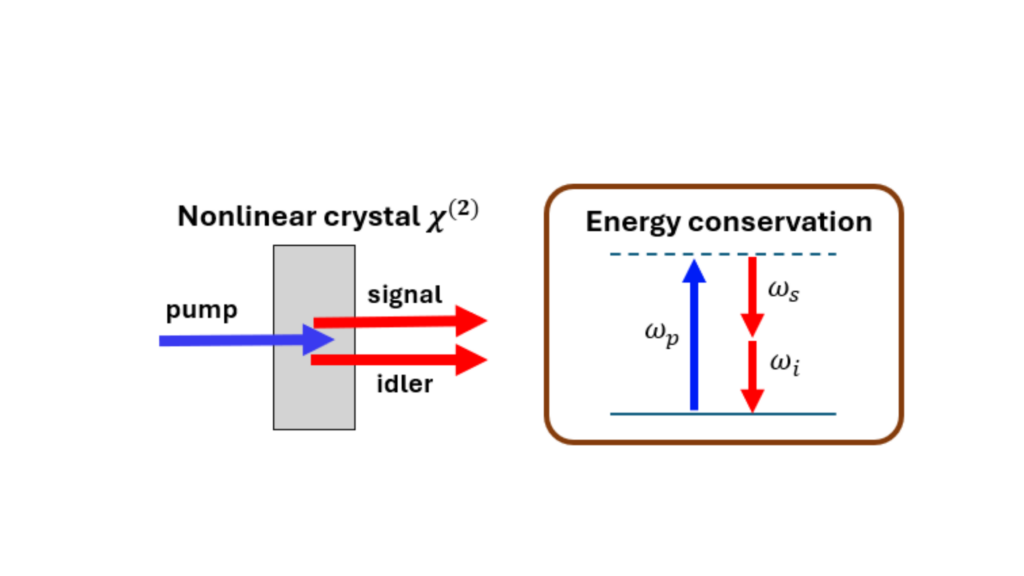
In 1992, J.D. Franson proposed an intriguing experiment (Fig. 2a). He suggested sending each photon through a different dispersive medium – one with normal dispersion, the other with anomalous dispersion – and then measuring their joint arrival times. Classically, one might expect the dispersion to broaden each photon’s wave-packet, resulting in a wider correlation profile. Surprisingly, Franson found that when the dispersions are opposite in sign, the broadening cancels out. The correlation remains as narrow as it was without dispersion!
This effect arises from the entangled nature of the photon pair. The joint two-photon state ensures that the dispersion experienced by one photon is precisely counteracted by that of its twin, a phenomenon described as nonlocal because the photons need not interact directly, and the two detectors might be very far away from each other. While classical analogs to this experiment exist [2], this cancellation highlights a distinctly quantum feature tied to entanglement, as the photons’ individual distortions are reconciled only through their shared state [3].
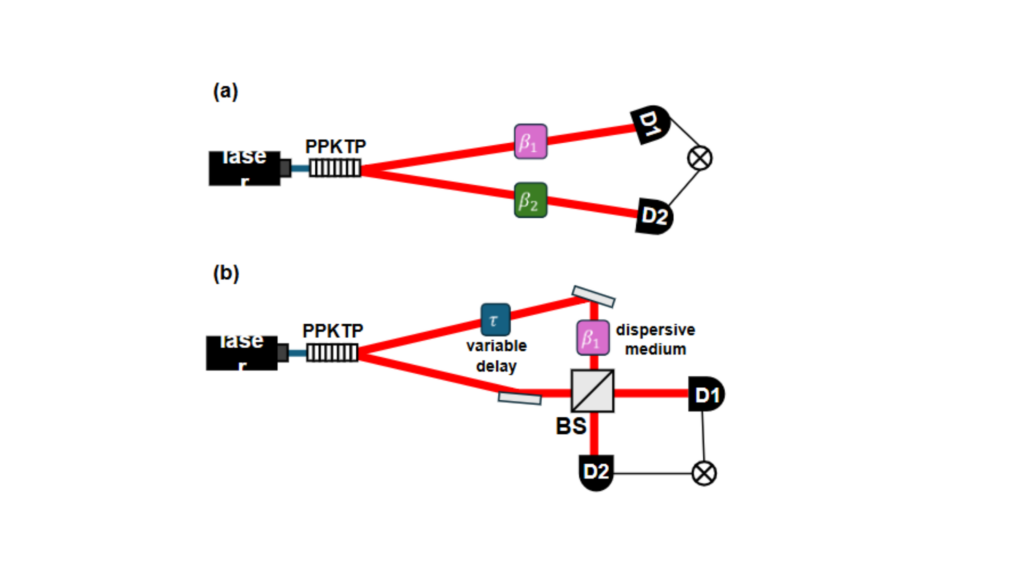
Steinberg’s Local Dispersion Cancellation
Shortly after Franson’s work, Aephraim Steinberg and colleagues proposed a complementary approach [4, 5]. In their experiment, only one of the entangled photons passes through a dispersive medium, while the other travels freely. The photons are then reunited at a beam splitter in a Hong-Ou-Mandel (HOM) interferometer (Fig. 2b), where identical photons exhibit a characteristic dip in coincidence counts due to destructive interference. Specifically, if two indistinguishable photons arrive at the beam splitter simultaneously, they will both exit in the same output port, thereby reducing coincidences and producing the HOM dip.
Once again, one might anticipate that dispersion would stretch the affected photon’s wave-packet, thereby reducing the overlap with its twin and broadening the HOM dip. However, Steinberg showed that the dip remains narrow, largely unaffected by the dispersion. This occurs because the two-photon amplitudes along possible paths through the beam splitter interfere in a way that cancels the dispersion’s impact. Remarkably, this setup also provided experimental evidence that a single photon travels through a material at its group velocity – the speed of the wave-packet’s peak – resolving a point of contention in photon propagation studies at the time.
Developments Since the 1990s
Since these pioneering experiments, dispersion cancellation has been explored in multiple contexts. The Franson effect has been demonstrated using diverse measurement methods [6, 7], and the dispersion cancellation concept has been extended to systems such as Mach-Zehnder interferometers [8] and optical cavities [9]. It has also been generalized to three-, or even multi-photon states [10], as well as to independent photons [11]. These advancements underscore the versatility of SPDC-generated photons and their utility in quantum optics research.
Implications and Applications
Dispersion cancellation illustrates how entanglement can preserve the integrity of quantum states against material-induced distortions. This property is valuable for quantum communication, where precise timing is critical, and for quantum imaging, where maintaining narrow correlations enhances resolution. At Raicol Crystals, we specialize in crafting nonlinear crystals that enable such experiments, providing researchers with the tools to explore and harness these effects. For more information on our quantum solutions, visit our quantum components page, or contact us directly.
References
[1] Franson, J. D. “Nonlocal cancellation of dispersion.” Physical Review A 45, no. 5 (1992): 3126.
[2] Shapiro, Jeffrey H. “Dispersion cancellation with phase-sensitive Gaussian-state light.” Physical Review A—Atomic, Molecular, and Optical Physics 81, no. 2 (2010): 023824.
[3] Franson, J. D. “Lack of dispersion cancellation with classical phase-sensitive light.” Physical Review A—Atomic, Molecular, and Optical Physics 81, no. 2 (2010): 023825.
[4] Steinberg, A. M., P. G. Kwiat, and R. Y. Chiao. “Dispersion cancellation in a measurement of the single-photon propagation velocity in glass.” Physical review letters 68, no. 16 (1992): 2421.
[5] Steinberg, Aephraim M., Paul G. Kwiat, and Raymond Y. Chiao. “Dispersion cancellation and high-resolution time measurements in a fourth-order optical interferometer.” Physical Review A 45, no. 9 (1992): 6659.
[6] Baek, So-Young, Young-Wook Cho, and Yoon-Ho Kim. “Nonlocal dispersion cancellation using entangled photons.” Optics express 17, no. 21 (2009): 19241-19252.
[7] O’Donnell, Kevin A. “Observations of dispersion cancellation of entangled photon pairs.” Physical review letters 106, no. 6 (2011): 063601.
[8] Larchuk, Todd S., Malvin C. Teich, and Bahaa EA Saleh. “Nonlocal cancellation of dispersive broadening in Mach-Zehnder interferometers.” Physical Review A 52, no. 5 (1995): 4145.
[9] Agarwal, Girish S., and S. Dutta Gupta. “Filtering of two-photon quantum correlations by optical cavities: Cancellation of dispersive effects.” Physical Review A 49, no. 5 (1994): 3954.
[10] Nodurft, I. C., S. U. Shringarpure, B. T. Kirby, T. B. Pittman, and J. D. Franson. “Nonlocal dispersion cancellation for three or more photons.” Physical Review A 102, no. 1 (2020): 013713.
[11] Im, Dong-Gil, Yosep Kim, and Yoon-Ho Kim. “Dispersion cancellation in a quantum interferometer with independent single photons.” Optics Express 29, no. 2 (2021): 2348-2363.
Author: Ori levin
At Raicol, as a world leader in the manufacture of PPKTP, our goal is to support the growing quantum industry and drive it forward as much as we can.
To support this goal, Raicol is continuously cooperating with research centers and leading universities worldwide to provide them with advanced quasi-phase-matching crystals that help them accomplish innovative research. At times, this requires us to push the envelope to improve our fabrication techniques and bring new capabilities.
In the past few years, Raicol has been dealing with repeating requests for PPKTP with low absorption, higher pump powers, and requests for shorter poling periods. We found some of these requirements intriguing and challenging and started researching different solutions to tackle these issues.
One of the leading challenges our customers face is dealing with gray tracking.
Gray tracking is a phenomenon where optical beams, above the average power threshold, propagate through PPKTP crystal and create photorefractive damage that leaves opaque areas, making the crystal useless.
In unpolled KTP which is used for nonlinear conversions, Raicol solved this issue by developing the HGTR KTP which was designed to support much higher power densities, however, HGTR KTP cannot be easily polled, thus does not offer a solution for the quantum industry.
To tackle this problem, Raicol has started a research project to develop a new product that will support a higher power-frequency conversion process
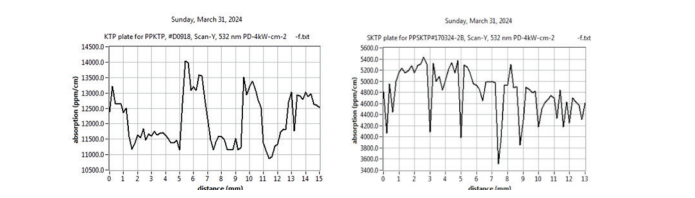
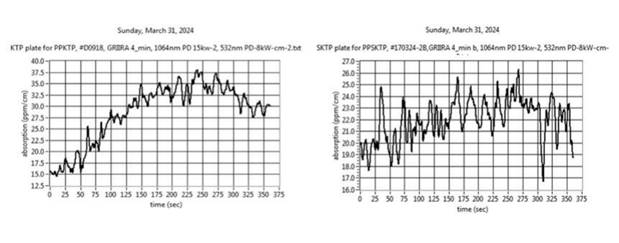
(such as SPDC) but at the same time, will not compromise the PPKTP absorption parameters. During the research, we have emphasized optimizing the Raicol bulk KTP absorption.
Following two years of research, Raicol developed a version of HGRK KTP that can be polled and created the new version of ppKTP which we called SPPKTP. The SppKTP supports up to 6 times the power as a standard PPKTP and has about 40% less absorption (ppm) in the 532 nm wavelength .
This technology finds numerous applications where even the smallest optical losses are highly detrimental or systems that can benefit from higher powers than typical KTP can support. Key examples include Optical Parametric Oscillators (OPOs), squeezed light sources, Quantum communications and quantum encryption (QKD), and high-power laser systems, where the high circulating power within the optical cavity demands an elevated optical damage threshold, exceptional crystal purity, and minimal losses to maintain efficient frequency conversion. In such systems, even minute losses can lead to reduced performance, thermal effects, and beam quality degradation.
In contrast, there are also applications operating at low power but requiring extremely low optical losses, such as systems with high Q-factor optical cavities. Here, losses directly influence the cavity linewidth, with narrow linewidths being essential for applications in high-precision metrology, laser stabilization, and quantum technologies.
Raicol’s SPPKTP crystals represent a significant advancement in nonlinear optical materials, driving innovation across diverse areas of photonics technology. Their breakthrough properties help unlock new possibilities in the field, from quantum applications to high-power laser systems
For detailed information about our sPPKTP crystals, download our product brochure or reach out to our team.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Dr. Noa Voloch Bloch and Ori Levin
Raicol, a renowned leader in PPKTP manufacturing, is committed to propelling the quantum industry forward through state-of-the-art solutions. Over the past few years, our relentless pursuit of excellence has led to significant enhancements in our manufacturing capabilities. Notably, we have dedicated substantial efforts to refining our proficiency in producing shorter poling periods.
While achieving short poling periods for individual elements with low yields is indeed feasible, the real challenge lies in scaling this capability for mass production and making it accessible to our valued customers at a competitive price point. Our engineer, Mr. Michael Schindler, has achieved a breakthrough by developing a process that enables extremely short poling periods (a full cycle of approximately 1 µm). As a result, we are proud to offer a standard poling period of less than 3 µm.
At Raicol, we remain committed to pushing the boundaries of what’s possible in the quantum industry, and our dedication to innovation continues to drive our success.
Narrow bandwidth SPDC
Raicol recently experienced a significant increase in demand for PPKTP crystals with extremely short poling periods. This demand was primarily driven by applications in narrow-band “Counter Propagation SPDC,” which can achieve bandwidths as low as 0.06 nm [1,2]. The importance of these narrow bandwidths lies in their potential for integrating SPDC sources with quantum memories, where matching the bandwidths of atomic transitions and exciting radiation is crucial. The relationship between crystal length and SPDC bandwidth is inverse, with longer crystals producing narrower bandwidths. While Raicol continues to improve its capabilities in this area, the company currently offers PPKTP crystals up to 30 mm in length. This development demonstrates Raicol’s ongoing commitment to advancing quantum technologies and meeting the evolving needs of the photonics industry. As the field of quantum optics continues to progress, Raicol remains dedicated to exploring innovative solutions and pushing the boundaries of PPKTP crystal manufacturing. The company’s efforts in producing crystals with extremely short poling periods and longer lengths are contributing to the advancement of quantum memory integration and other cutting-edge applications in quantum technologies.
Production validation to short poling
As a leader in nonlinear crystal manufacturing we maintain rigorous quality control procedures, especially when developing new crystals or cutting-edge technologies. When trying to implement short poling we faced challenge in characterizing and validating short-polled KTP crystals. While Raicol’s measuring testing systems are typically designed for forward-propagating Second Harmonic Generation (SHG) and Spontaneous Parametric Down-Conversion (SPDC) across various wavelengths. However, the short-period polled KTP crystals presented a distinct obstacle. The absence of forward SHG/SPDC processes corresponding to the short period, due to their occurrence near the edge of the KTP transmission window, made conventional collinear second harmonic processes unsuitable for evaluation of 1.2 µm polled crystals. This situation underscores the complexity of validating advanced crystal technologies and highlights Raicol’s commitment to ensuring product performance through innovative testing methodologies.
A. Backward second harmonic generation
There are two distinct types of collinear second harmonic generation SHG processes [3]: forward and backward propagation:
Forward Second Harmonic Generation: In this process, the beam at the doubled frequency propagates in the same direction as the beam at the fundamental frequency. In the case of PPKTP the shortest poling period enabling efficient frequency doubling from 800 nm pump to 400 nm is approximately 3 µm.
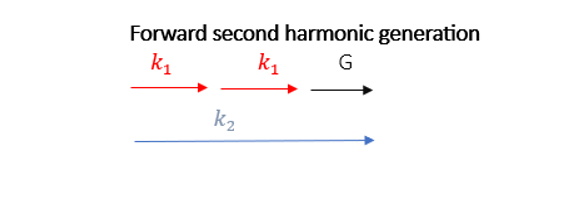
Backward Second Harmonic Generation: In this process, the generated wave propagates in the opposite direction of the pump.
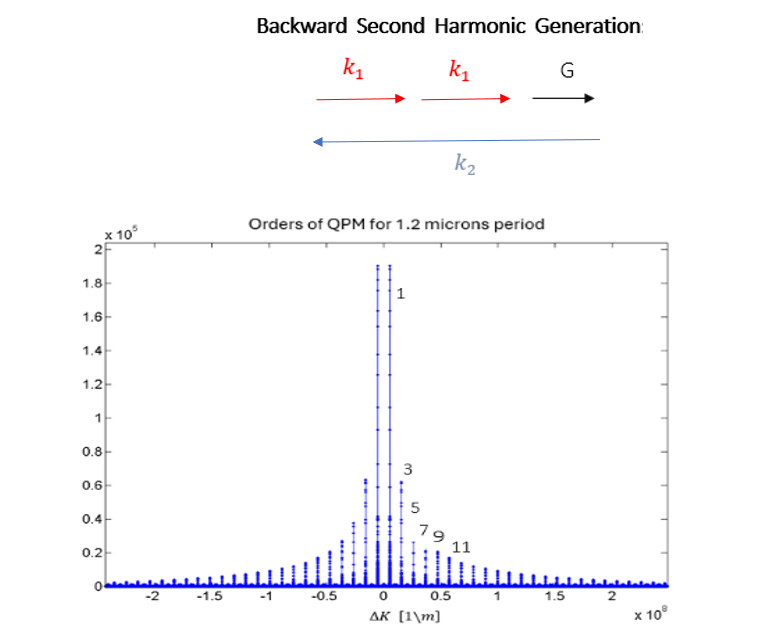
However, the periods necessary for efficient backward second harmonic generation for visible wavelengths are extremely short and pose significant manufacturing challenges. For example, generating a second harmonic of 829 nm light in the first-order QPM requires a period of 0.109 µm.
B. Backward propagation test bench
In order to characterize our 1.2 short poling crystals we measure SH backward propagation, we evaluated the ΔK that matches the phase matching values of 1.2 µm grating periods. For the ΔK values shown in the graph there is no forward process. But for the 829 nm converted to 414.4 nm at 33 deg PPKTP
The ΔK is 5.754⋅10^7 [1/m] specifically suites phase matching of the 11-th order shown in the graph. Backward second harmonic generation of 829 nm converted to 414.5nm [3].
To overcome this challenge, we implement a backward propagation test system, as outlined below: The 829 nm pump beam enters the crystal and the SH which propagates backward is deflected by a dichroic mirror to the detector.

[1] Liu, YC., Guo, DJ., Ren, KQ. et al. Observation of frequency-uncorrelated photon pairs generated by counter-propagating spontaneous parametric down-conversion. Sci Rep 11, 12628 (2021).
[2] Zhang, H., Jin, XM., Yang, J. et al. Preparation and storage of frequency-uncorrelated entangled photons from cavity-enhanced spontaneous parametric downconversion. Nature Photon 5, 628–632 (2011).
[3] S. Moscovich, A. Arie, R. Urenski, A. Agronin, G. Rosenman and T. Rosenwaks, “Noncollinear second harmonic generation in sub-micrometer poled RbTiOPO4”, Optics Express, 12, 2236-2242 (2004).
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
Quantum and classical ghost imaging
Ghost imaging, one of the first imaging techniques using quantum light, has captivated researchers since its inception in the mid-1990s. The concept of ghost imaging was first demonstrated in 1995 by Pittman et al. [1], using quantum light generated via spontaneous parametric down-conversion (SPDC), a nonlinear optical process that converts a pump photon into two lower-energy entangled photons.
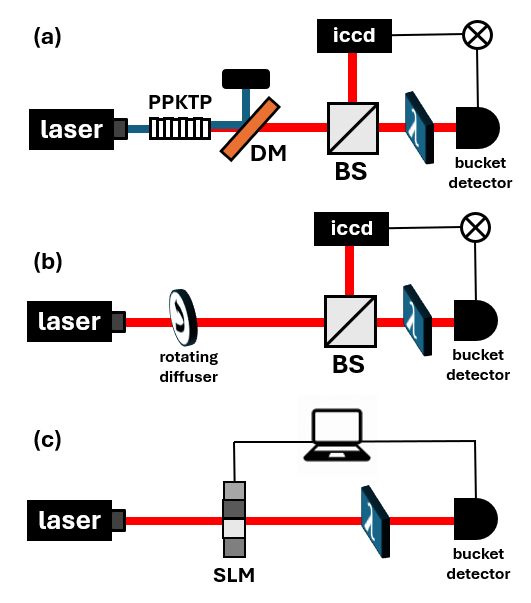
In this experiment (Fig. 1a), the spatially entangled photons are separated, with one photon propagating through an object and being collected using a bucket detector with no spatial resolution, while the idler photon is sent to a multi-pixeled camera. By measuring coincidence events between the bucket detector and the camera, the object is reconstructed, despite the fact that the photons detected by the camera did not directly interact with it! This nonlocal characteristic led to the term “ghost imaging.”
The crux of this technique lies in the spatial correlations of the two photons: areas that are blocked by the object will not reach the bucket detector, so coincidence events will not occur with the corresponding pixels in the camera. But one must remember: correlations do not necessarily imply entanglement! Does quantum entanglement play a critical role in this technique? This was the subject of a debate that lasted several years.
In [2], for instance, theoretical arguments were presented, suggesting that entanglement is intrinsic to ghost imaging. However, in 2002, Bennik et al. [3] demonstrated ghost imaging using two classically correlated beams, randomly deflected at different angles. Others explored similar classical correlations using a rotating diffuser [4], generating correlated pseudo-thermal light (Fig. 1b).
Computational ghost imaging
An important fruit of this debate was that of computational ghost imaging, proposed by Shapiro [5], and demonstrated by Bromberg et al. [6]. In this method, only a single detector is used, and the high-resolution camera is replaced by a computation of the propagating field which is shaped using a spatial light modulator (Fig. 1c). The key point here is that we know everything about the photon propagating to the camera, so we can utilize this knowledge computationally and get rid of the physical camera. The object image is obtained by correlating the intensities measured by the bucket detector with the calculated field at the object plane.
While this computational approach already simplified the experimental setup, researchers soon realized [7] that the number of measurements could be significantly reduced by leveraging modern image processing techniques, particularly those that exploit prior knowledge about the image structure. Remarkably, for most imaging tasks, such information exists: natural images are sparse, that is, they contain many coefficients close to or equal to zero when represented in an appropriate basis. This property of natural images is at the core of modern lossy image compression algorithms, such as JPEG. The field of compressed sensing exploits this sparsity/compressibility to reduce the number of measurements needed for faithful image recovery. Utilizing this technique reduces the number of measurements required for a faithful reconstruction by an order of magnitude.
Current state and future directions
The fact that computational ghost imaging uses only a single detector provides experimental evidence that pseudothermal ghost imaging does not inherently rely on nonlocal quantum correlations. It is now also recognized that the quantum and classical methods produce images of a similar resolution. The main advantage of utilizing quantum light for ghost imaging is found at low light levels, at which the quantum modality exhibits greater visibility and a greater signal-to-noise ratio [8]. This could be especially important when imaging samples that are sensitive to high light levels. Further details comparing the classical and quantum modalities may be found in [9].
Almost 30 years since its first demonstration, many extensions, applications, and modalities of ghost imaging are still being explored. Are you interested in ghost imaging with quantum light? Or perhaps want to explore other use cases for quantum entanglement? Please check out our PPKTP crystal and BBO crystals, used for generating entangled photons, and join the conversation!
[1] Pittman, Todd B., Y. H. Shih, D. V. Strekalov, and Alexander V. Sergienko. “Optical imaging by means of two-photon quantum entanglement.” Physical Review A 52, no. 5 (1995): R3429.
[2] Abouraddy, Ayman F., Bahaa EA Saleh, Alexander V. Sergienko, and Malvin C. Teich. “Role of entanglement in two-photon imaging.” Physical review letters 87, no. 12 (2001): 123602.
[3] Bennink, Ryan S., Sean J. Bentley, and Robert W. Boyd. ““Two-photon” coincidence imaging with a classical source.” Physical review letters 89, no. 11 (2002): 113601.
[4] Valencia, Alejandra, Giuliano Scarcelli, Milena D’Angelo, and Yanhua Shih. “Two-photon imaging with thermal light.” Physical review letters 94, no. 6 (2005): 063601.
[5] Shapiro, Jeffrey H. “Computational ghost imaging.” Physical Review A—Atomic, Molecular, and Optical Physics 78, no. 6 (2008): 061802.
[6] Bromberg, Yaron, Ori Katz, and Yaron Silberberg. “Ghost imaging with a single detector.” Physical Review A—Atomic, Molecular, and Optical Physics 79, no. 5 (2009): 053840.
[7] Katz, Ori, Yaron Bromberg, and Yaron Silberberg. “Compressive ghost imaging.” Applied Physics Letters 95, no. 13 (2009).
[8] Moreau, Paul-Antoine, Ermes Toninelli, Thomas Gregory, and Miles J. Padgett. “Imaging with quantum states of light.” Nature Reviews Physics 1, no. 6 (2019): 367-380.
[9] Erkmen, Baris I., and Jeffrey H. Shapiro. “Ghost imaging: from quantum to classical to computational.” Advances in Optics and Photonics 2, no. 4 (2010): 405-450.
Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Author: Ronen Shekel
In a previous post, we talked about how periodic poling provides quasi-phase-matching, its various benefits, and the control it provides over different SPDC parameters.
SPDC light is used for numerous applications, such as quantum imaging, quantum communications, and quantum computing. As these applications mature, it becomes increasingly important to have better and stronger control over the properties of the generated quantum states, such as their purity and fidelity. For instance, for some quantum computation or communication applications one would like to generate specific entangled states, such as Bell states or cluster states [1]. However, for a heralded single-photon application, one would like the SPDC process to result in a separable state, since heralding a photon out of an entangled pair will result in a single photon in a mixed state.
A promising approach for achieving such control is to create more sophisticated crystals by further tailoring their poling and realizing aperiodic poling and custom duty cycles. For example, one could create a chirping grating, where the poling interval is linearly varied between the entrance and end facets of the crystal. Such a method has been employed for the generation of an ultrabroad-spectrum in SPDC light [2], achieving a record-breaking narrow Hong-Ou-Mandel (HOM) dip.
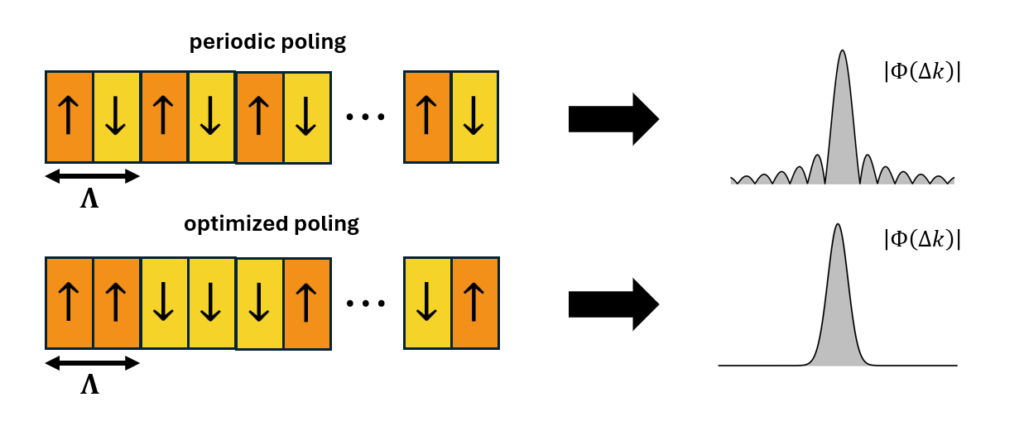
Another example of engineering poling is given in [3, 4]. In the usual case, the nonlinearity that the pump pulse experiences is turned on suddenly as the pump enters the crystal and turned off just as suddenly as the pump exits the crystal. This results in sinc side lobes in the joint spectrum amplitude (JSA) of the generated states. What it means is that part of the SPDC photon pairs are generated at a combination of different wavelengths, resulting in different quantum states. Since for high visibility quantum interference and superposition we need photons which are well defined in their physical properties, we need to find an engineering method which will concentrate the generated SPDC photon pairs into one well defined quantum state. Here, it is shown that a special type of domain engineering allows an apodization of the spectrum, the removal of the sinc sidelobes (Fig. 1).
As evident by the large HOM dip visibility, the states generated from this apodised crystal are highly pure and indistinguishable. Such purity and indistinguishability are of utmost importance for advanced photonic technologies, which rely on a high number of successive two-photon interference events.
Having control on the crystal spectral properties is of special interest when generating high-dimensional quantum states and novel entanglement possibilities [6] . Such states are gaining growing interest in recent years due to their higher information capacity and their improved resilience to noise [5]. They come in two flavors: spectral entanglement and spatial entanglement. As opposed to polarization encoding, both cases allow the encoding of high-dimensional information, enabling each photon to carry more information. Encoding in the spectrum enjoys the fact that such states experience virtually no decoherence. Encoding in the spatial domain is attractive because it is easy to control and manipulate using the mature technology of spatial light modulators. In both cases, aperiodic polling, together with optimizing the pump beam that stimulates the SPDC process, has been shown to allow greater control over the generated states.
In [6], a variety of spectrally encoded states, such as Bell states and two-qutrit states, have been generated using domain engineering, along with the modulation of a broadband pulsed pump. Using this method, there is no need to filter the (very few) SPDC photons after the generation process, since shaping the pump and crystal already enables the generation of the desired joint spectrum directly. Specifically, the pump modulation was done via a simple technique, using only passive optical elements such as birefringent wedges and waveplates. In general, the pump spectrum could be shaped even more flexibly using diffraction gratings and spatial light modulators [7].
A similar two-dimensional approach is shown in [8], but in the spatial domain. A detailed physical model, together with a machine learning framework, finds optimal 3-dimensional crystal structures as well as tailored pump shapes that generate arbitrary spatially encoded states. In [9] this has been shown experimentally, generating a spatial Bell state in the Hermite-Gauss basis, by engineering the nonlinear crystal.
Raicol is a world leader in both periodic and aperiodic poling of nonlinear crystals, and provides aperiodically poled KTP crystals (APKTP) that increase the spectral purity and indistinguishability of the emitted photon pairs at telecom wavelengths. We also provide tailored solutions for crystals with aperiodic poling. Please contact us to discuss your application and how we can help you use state-of-the-art crystals to achieve your goals.
[1] Briegel, Hans J., et al. “Measurement-based quantum computation.” Nature Physics 5.1 (2009): 19-26.
[2] Nasr, M.B., Carrasco, S., Saleh, B.E., Sergienko, A.V., Teich, M.C., Torres, J.P., Torner, L., Hum, D.S. and Fejer, M.M., 2008. Ultrabroadband biphotons generated via chirped quasi-phase-matched optical parametric down-conversion. Physical review letters, 100(18), p.183601.
[3] Graffitti, F., Barrow, P., Proietti, M., Kundys, D. and Fedrizzi, A., 2018. Independent high-purity photons created in domain-engineered crystals. Optica, 5(5), pp.514-517.
[4] Dosseva, Annamaria, Łukasz Cincio, and Agata M. Brańczyk. “Shaping the joint spectrum of down-converted photons through optimized custom poling.” Physical Review A 93.1 (2016): 013801.
[5] Ecker, Sebastian, Frédéric Bouchard, Lukas Bulla, Florian Brandt, Oskar Kohout, Fabian Steinlechner, Robert Fickler et al. “Overcoming noise in entanglement distribution.” Physical Review X 9, no. 4 (2019): 041042.
[6] Shukhin, Anatoly, Inbar Hurvitz, Sivan Trajtenberg-Mills, Ady Arie, and Hagai Eisenberg. “Two-dimensional control of a biphoton joint spectrum.” Optics Express 32, no. 6 (2024): 10158-10174.
[7] Ansari, Vahid, et al. “Heralded generation of high-purity ultrashort single photons in programmable temporal shapes.” Optics express 26.3 (2018): 2764-2774.
[8] Rozenberg, Eyal, Aviv Karnieli, Ofir Yesharim, Joshua Foley-Comer, Sivan Trajtenberg-Mills, Daniel Freedman, Alex M. Bronstein, and Ady Arie. “Inverse design of spontaneous parametric downconversion for generation of high-dimensional qudits.” Optica 9, no. 6 (2022): 602-615.
[9] Yesharim, Ofir, Shaul Pearl, Joshua Foley-Comer, Irit Juwiler, and Ady Arie. “Direct generation of spatially entangled qudits using quantum nonlinear optical holography.” Science Advances 9, no. 8 (2023): eade7968.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
Home » Articles
Author: Ronen Shekel
The generation of pure nonclassical states of light is one of the most important goals of optical quantum information science. A popular and versatile source for creating such states is spontaneous parametric down-conversion (SPDC) – a nonlinear process where a pump beam hits a nonlinear crystal and produces pairs of lower energy photons [1]. Indeed, in the past several decades, SPDC has been widely used for generating heralded single photons and entangled photon pairs, used for applications such as quantum communications and quantum metrology.
For the SPDC process to be efficient, both energy and momentum must be conserved, as depicted in Fig. 1a. In an ideal scenario without chromatic dispersion, phase matching would work trivially, since the frequency and wavevector are simply related by a factor of the speed of light. However, real optical materials exhibit chromatic dispersion, which means that the refractive index varies with wavelength, resulting in a wavevector mismatch Δk_z.
One way to overcome the wavevector mismatch, named birefringent phase matching [2], is by taking advantage of the difference in phase accumulation for different polarizations. In this technique, the polarization of the pump and generated photons are chosen such that this effect will compensate for the chromatic dispersion.
A second popular technique, named quasi-phase matching, was proposed as early as 1962 [3]. This technique resolves the mismatch by splitting the crystal into domains, where alternating domains have nonlinear coefficients of opposite signs (Fig. 1b). This technique may be understood using a phasor diagram (Fig. 1c). The wavevector mismatch causes the phases to accumulate differently, and after a finite propagation distance, they will begin to interfere destructively. With quasi-phase matching, the domain periodicity Λ is chosen such that when the process reaches the destructive interference region, the sign of the phasors are flipped, and the process is allowed to continue to build constructively.
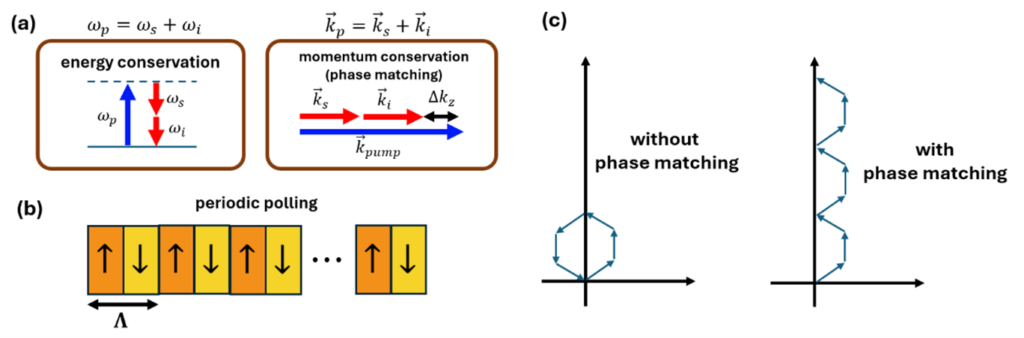
Interestingly, it took until the mid-1980s for this technique to become widespread experimentally [4], using periodic polling. This is because the creation of such domains is challenging, and typically uses ferroelectric domain engineering [5]. This involves the application of a strong electric field to a ferroelectric crystal via patterned electrodes on the crystal surface. This strong field changes the crystal orientation under the electrodes and thus reverses the sign of its nonlinear coefficient. Periodic poling is especially challenging to perform on large-aperture crystals and with small poling periods.
The advantages of quasi-phase matching are that it allows the use of materials with stronger nonlinear coefficients, avoids spatial walk-off, and does not add requirements on the polarization of the different fields. Another advantage is that by tailoring the poling period, different SPDC parameters may be controlled.
For example, as has been shown in [6], using different poling periods could determine whether a type-0 or type-II process will take place. A Type-0 process, where the pump and both generated photons have the same polarization, could be desirable due to its high pair-generation rate. However, it is relatively sensitive to temperature changes and has a large bandwidth. In a type-II process, the two resulting photons have orthogonal polarization, and a narrow spectrum, but the process tends to be weaker.
It is very important to understand the specific application and desired figure of merit before choosing a crystal configuration. For instance, is the total flux the important measure? Or perhaps the total flux per nm of wavelength? Is spatial entanglement a desired feature or something to avoid? Depending on the exact application, a different configuration of pump beam, crystal dimensions, temperature, and poling periodicity may be the best fit [7].
Raicol Crystals is a world-leader in quasi phase matched crystals, and provides periodically poled nonlinear crystals such as PPLN, PPKTP, and PPSLT, allowing a wide range of periodicities and crystal dimensions. Please contact us for further details! We also provide aperiodically poled KTP (APKTP) crystals, which allow even further control of the resulting quantum state. This will be the subject of another post, so stay tuned!
[1] Walborn, S.P., Monken, C.H., Pádua, S. and Ribeiro, P.S., 2010. Spatial correlations in parametric down-conversion. Physics Reports, 495(4-5), pp.87-139.
[2] Boyd, R.W., Gaeta, A.L. and Giese, E., 2008. Nonlinear optics.
[3] Armstrong, J. A., N. Bloembergen, J. Ducuing, and Peter S. Pershan. “Interactions between light waves in a nonlinear dielectric.” Physical review 127, no. 6 (1962): 1918.
[4] R. Paschotta, article on “Quasi-phase Matching” in the RP Photonics Encyclopedia, retrieved 2024-08-21, https://doi.org/10.61835/kj9
[5] Yamada, M., Nada, N., Saitoh, M. and Watanabe, K., 1993. First‐order quasi‐phase matched LiNbO3 waveguide periodically poled by applying an external field for efficient blue second‐harmonic generation. Applied Physics Letters, 62(5), pp.435-436.
[6] Steinlechner, F., Gilaberte, M., Jofre, M., Scheidl, T., Torres, J.P., Pruneri, V. and Ursin, R., 2014. Efficient heralding of polarization-entangled photons from type-0 and type-II spontaneous parametric downconversion in periodically poled KTiOPO 4. JOSA B, 31(9), pp.2068-2076.
[7] Schneeloch, J., Knarr, S.H., Bogorin, D.F., Levangie, M.L., Tison, C.C., Frank, R., Howland, G.A., Fanto, M.L. and Alsing, P.M., 2019. Introduction to the absolute brightness and number statistics in spontaneous parametric down-conversion. Journal of Optics, 21(4), p.043501.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates.
Author: Ronen Shekel
One of the most remarkable features of quantum theory is entanglement, where quantum systems show nonlocal correlations between particles or photons that are impossible to explain using classical physics. This can famously be demonstrated, for example, by violating a Bell inequality [1, 2]. While in many cases entanglement between two-level systems (qubits) is discussed, high-dimensional entanglement between multi-level systems provides an even richer structure.
High-dimensional entangled states are attractive because they have a greater information capacity, and also show increased resistance to noise and losses [3]. Additionally, it is relatively straightforward to generate high-dimensional entangled states using spontaneous parametric down-conversion (SPDC), and to shape them using liquid crystal spatial light modulators [4].
In SPDC [5], a strong plane-wave pump beam impinges upon a nonlinear crystal such as PPKTP (Periodic polled KTP). With some probability, related to the crystal’s nonlinear coefficients, a pump photon will be annihilated, and two entangled photons will be created (Fig. 1a). Since energy must be conserved, the frequencies of these two photons must sum to that of the pump photon, and here we will assume the degenerate case, where they have the same frequency (Fig. 1b). Since momentum must be conserved, the wave vectors of the created photons must add up to that of the pump photon, which is pointing in a specific direction, since the pump is a plane wave. Consequently, the two photons will have anti-correlations in their transverse momentum (Fig. 1c). This means that if one photon is emitted with a certain angle, its twin will be emitted in the opposite direction with respect to the pump beam.
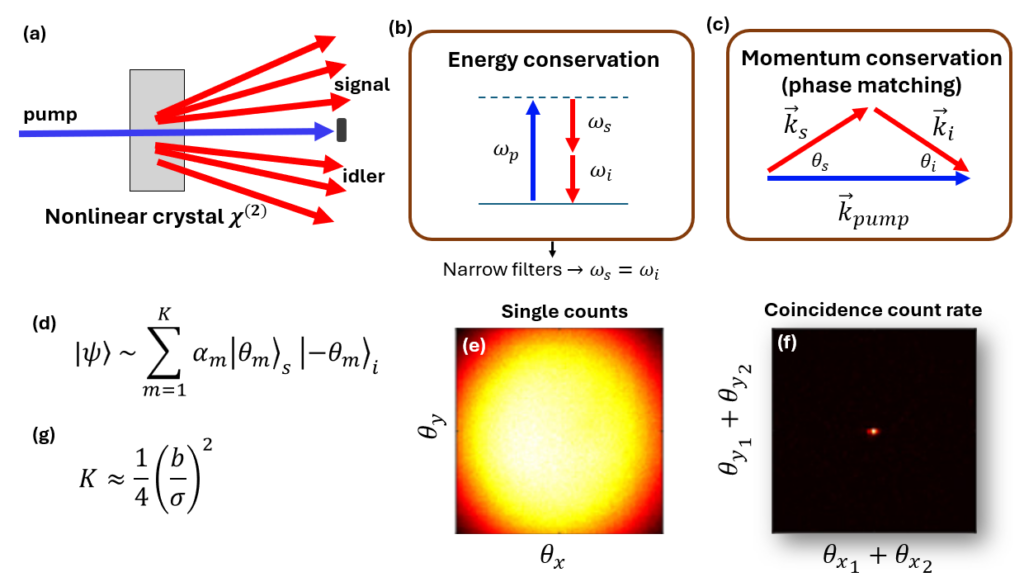
In fact, the generated state of these two photons is a coherent superposition of emission in these different angles, each photon in an opposite direction, with coefficients that depend on the exact phase-matching conditions (Fig. 1d), and typically depend on the angles like a sinc function [5]. These correlations may be measured in the far-field. Using a simple camera, we observe the “single counts”, which is the average intensity of photons emitted in all the directions permitted by the phase matching, which may be a rather wide region (Fig. 1e). Performing coincidence measurements, however, will reveal that given that one photon was measured in a certain angle, the twin photon will always be strongly correlated, and will be found in a much smaller “coincidence region” (Fig. 1f).
The ratio between the coincidence region and the single counts region quantifies the number of distinct modes in the quantum superposition, which is related to its Schmidt rank [6, 7] (Fig. 1g). Hence, to tailor the spatial entanglement properties in SPDC, one should consider both the width of the phase matching function (controlling the single counts region) and the strength of the correlations, and plan an optical setup accordingly.
Specifically, the angular width b of the phase matching sinc function, or equivalently, the angular range allowed by the SPDC process, is determined by the pump wavelength λ_p, and by the crystal thickness L, and is approximately. √(λ_p/L) Thus, while using a thin crystal will result in smaller SPDC flux due to a shorter interaction length, it will typically allow a larger range of emission angles, and will generate highly spatially entangled states.
Conversely, the width of the coincidence region is determined by the angular spectrum of the pump, σ. Indeed, for a plane-wave pump with a single well-defined momentum vector, we expect perfect correlations. However, a finite pump beam will necessarily contain many different angles, which will allow an angle mismatch in the momentum conservation. This is referred to more generally as the transfer of angular spectrum from the pump to the SPDC correlations [8].
In conclusion, having a wide pump beam with a narrow angular spectrum, and using a thin crystal, will increase the dimensionality of the SPDC spatial entanglement. The same reasoning about the number of effective modes can equivalently be carried out in the near-field: A wide pump beam yields a correspondingly large emission area of the SPDC photons, and a thin crystal results in each pair of photons being strongly spatially correlated at the output of the crystal due to the small propagation distance traveled from their point of generation [6, 9].
Of course, one doesn’t always want high-dimensional spatial entanglement. For instance, in many cases, SPDC photons are coupled into single-mode fibers. In such a case, we would like to generate only a single spatial mode to get good coupling to the fiber. A good rule of thumb for this is to set the Rayleigh length of the pump to be the length of the crystal.
At Raicol, we provide a variety of nonlinear crystals with a rich range of parameters, allowing you to design your optical setup exactly for your needs. We also provide custom-made periodic polled crystals with specially tailored polling, allowing the shaping of the two-photon joint spectral intensity [10], which will be the subject of a different post. For more information, please visit our products page, and contact us if you have any questions.
[1] Bell, John S. “On the einstein podolsky rosen paradox.” Physics Physique Fizika 1, no. 3 (1964): 195.
[2] Brunner, Nicolas, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. “Bell nonlocality.” Reviews of modern physics 86, no. 2 (2014): 419.
[3] Ecker, Sebastian, Frédéric Bouchard, Lukas Bulla, Florian Brandt, Oskar Kohout, Fabian Steinlechner, Robert Fickler et al. “Overcoming noise in entanglement distribution.” Physical Review X 9, no. 4 (2019): 041042.
[4] Defienne, Hugo, Matthew Reichert, and Jason W. Fleischer. “Adaptive quantum optics with spatially entangled photon pairs.” Physical review letters 121, no. 23 (2018): 233601.
[5] Walborn, Stephen P., C. H. Monken, S. Pádua, and PH Souto Ribeiro. “Spatial correlations in parametric down-conversion.” Physics Reports 495, no. 4-5 (2010): 87-139.
[6] Lib, Ohad. “Utilizing the Spatial Degree of Freedom of Entangled Photons for High-Dimensional Quantum Information Processing”, PhD thesis.
[7] Law, C. K., and J. H. Eberly. “Analysis and interpretation of high transverse entanglement in optical parametric down conversion.” Physical review letters 92, no. 12 (2004): 127903.
[8] Monken, Carlos Henrique, PH Souto Ribeiro, and Sebastiao Pádua. “Transfer of angular spectrum and image formation in spontaneous parametric down-conversion.” Physical Review A 57, no. 4 (1998): 3123.
[9] Schneeloch, James, and John C. Howell. “Introduction to the transverse spatial correlations in spontaneous parametric down-conversion through the biphoton birth zone.” Journal of Optics 18, no. 5 (2016): 053501.
[10] Shukhin, Anatoly, Inbar Hurvitz, Sivan Trajtenberg-Mills, Ady Arie, and Hagai Eisenberg. “Two-dimensional control of a biphoton joint spectrum.” Optics Express 32, no. 6 (2024): 10158-10174.
Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.
