Author: Ronen Shekel

In a previous post, we talked about how periodic poling provides quasi-phase-matching, its various benefits, and the control it provides over different SPDC parameters.

SPDC light is used for numerous applications, such as quantum imaging, quantum communications, and quantum computing. As these applications mature, it becomes increasingly important to have better and stronger control over the properties of the generated quantum states, such as their purity and fidelity. For instance, for some quantum computation or communication applications one would like to generate specific entangled states, such as Bell states or cluster states [1]. However, for a heralded single-photon application, one would like the SPDC process to result in a separable state, since heralding a photon out of an entangled pair will result in a single photon in a mixed state.

A promising approach for achieving such control is to create more sophisticated crystals by further tailoring their poling and realizing aperiodic poling and custom duty cycles. For example, one could create a chirping grating, where the poling interval is linearly varied between the entrance and end facets of the crystal. Such a method has been employed for the generation of an ultrabroad-spectrum in SPDC light [2], achieving a record-breaking narrow Hong-Ou-Mandel (HOM) dip.

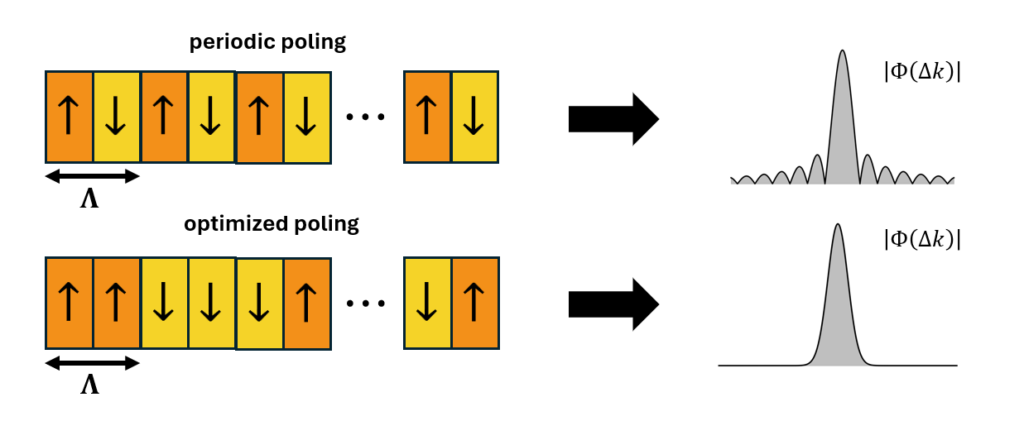
Another example of engineering poling is given in [3, 4]. In the usual case, the nonlinearity that the pump pulse experiences is turned on suddenly as the pump enters the crystal and turned off just as suddenly as the pump exits the crystal. This results in sinc side lobes in the joint spectrum amplitude (JSA) of the generated states. What it means is that part of the SPDC photon pairs are generated at a combination of different wavelengths, resulting in different quantum states. Since for high visibility quantum interference and superposition we need photons which are well defined in their physical properties, we need to find an engineering method which will concentrate the generated SPDC photon pairs into one well defined quantum state.  Here, it is shown that a special type of domain engineering allows an apodization of the spectrum, the removal of the sinc sidelobes (Fig. 1).

  As evident by the large HOM dip visibility, the states generated from this apodised crystal are highly pure and indistinguishable. Such purity and indistinguishability are of utmost importance for advanced photonic technologies, which rely on a high number of successive two-photon interference events.

Figure 1 - Regular periodic poling results in side lobes of the sinc phase-matching function. Using optimized poling allows us to overcome this and get a cleaner phase-matching function

Having control on the crystal spectral properties  is of special interest when generating high-dimensional quantum states and novel entanglement possibilities [6] . Such states are gaining growing interest in recent years due to their higher information capacity and their improved resilience to noise [5]. They come in two flavors: spectral entanglement and spatial entanglement. As opposed to polarization encoding, both cases allow the encoding of high-dimensional information, enabling each photon to carry more information. Encoding in the spectrum enjoys the fact that such states experience virtually no decoherence. Encoding in the spatial domain is attractive because it is easy to control and manipulate using the mature technology of spatial light modulators. In both cases, aperiodic polling, together with optimizing the pump beam that stimulates the SPDC process, has been shown to allow greater control over the generated states.

In [6], a variety of spectrally encoded states, such as Bell states and two-qutrit states, have been generated using domain engineering, along with the modulation of a broadband pulsed pump. Using this method, there is no need to filter the (very few) SPDC photons after the generation process, since shaping the pump and crystal already enables the generation of the desired joint spectrum directly. Specifically, the pump modulation was done via a simple technique, using only passive optical elements such as birefringent wedges and waveplates. In general, the pump spectrum could be shaped even more flexibly using diffraction gratings and spatial light modulators [7].

A similar two-dimensional approach is shown in [8], but in the spatial domain. A detailed physical model, together with a machine learning framework, finds optimal 3-dimensional crystal structures as well as tailored pump shapes that generate arbitrary spatially encoded states. In [9] this has been shown experimentally, generating a spatial Bell state in the Hermite-Gauss basis, by engineering the nonlinear crystal.

Raicol is a world leader in both periodic and aperiodic poling of nonlinear crystals, and provides aperiodically poled KTP crystals (APKTP) that increase the spectral purity and indistinguishability of the emitted photon pairs at telecom wavelengths. We also provide tailored solutions for crystals with aperiodic poling. Please contact us to discuss your application and how we can help you use state-of-the-art crystals to achieve your goals.

[1] Briegel, Hans J., et al. “Measurement-based quantum computation.” Nature Physics 5.1 (2009): 19-26.

[2] Nasr, M.B., Carrasco, S., Saleh, B.E., Sergienko, A.V., Teich, M.C., Torres, J.P., Torner, L., Hum, D.S. and Fejer, M.M., 2008. Ultrabroadband biphotons generated via chirped quasi-phase-matched optical parametric down-conversion. Physical review letters, 100(18), p.183601.

[3] Graffitti, F., Barrow, P., Proietti, M., Kundys, D. and Fedrizzi, A., 2018. Independent high-purity photons created in domain-engineered crystals. Optica, 5(5), pp.514-517.

[4] Dosseva, Annamaria, Łukasz Cincio, and Agata M. Brańczyk. “Shaping the joint spectrum of down-converted photons through optimized custom poling.” Physical Review A 93.1 (2016): 013801.

[5] Ecker, Sebastian, Frédéric Bouchard, Lukas Bulla, Florian Brandt, Oskar Kohout, Fabian Steinlechner, Robert Fickler et al. “Overcoming noise in entanglement distribution.” Physical Review X 9, no. 4 (2019): 041042.

[6] Shukhin, Anatoly, Inbar Hurvitz, Sivan Trajtenberg-Mills, Ady Arie, and Hagai Eisenberg. “Two-dimensional control of a biphoton joint spectrum.” Optics Express 32, no. 6 (2024): 10158-10174.

[7] Ansari, Vahid, et al. “Heralded generation of high-purity ultrashort single photons in programmable temporal shapes.” Optics express 26.3 (2018): 2764-2774.

[8] Rozenberg, Eyal, Aviv Karnieli, Ofir Yesharim, Joshua Foley-Comer, Sivan Trajtenberg-Mills, Daniel Freedman, Alex M. Bronstein, and Ady Arie. “Inverse design of spontaneous parametric downconversion for generation of high-dimensional qudits.” Optica 9, no. 6 (2022): 602-615.

[9] Yesharim, Ofir, Shaul Pearl, Joshua Foley-Comer, Irit Juwiler, and Ady Arie. “Direct generation of spatially entangled qudits using quantum nonlinear optical holography.” Science Advances 9, no. 8 (2023): eade7968.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

 

Author: Ronen Shekel

The generation of pure nonclassical states of light is one of the most important goals of optical quantum information science. A popular and versatile source for creating such states is spontaneous parametric down-conversion (SPDC) – a nonlinear process where a pump beam hits a nonlinear crystal and produces pairs of lower energy photons [1]. Indeed, in the past several decades, SPDC has been widely used for generating heralded single photons and entangled photon pairs, used for applications such as quantum communications and quantum metrology.

For the SPDC process to be efficient, both energy and momentum must be conserved, as depicted in Fig. 1a. In an ideal scenario without chromatic dispersion, phase matching would work trivially, since the frequency and wavevector are simply related by a factor of the speed of light. However, real optical materials exhibit chromatic dispersion, which means that the refractive index varies with wavelength, resulting in a wavevector mismatch Δk_z.

One way to overcome the wavevector mismatch, named birefringent phase matching [2], is by taking advantage of the difference in phase accumulation for different polarizations. In this technique, the polarization of the pump and generated photons are chosen such that this effect will compensate for the chromatic dispersion.

A second popular technique, named quasi-phase matching, was proposed as early as 1962 [3]. This technique resolves the mismatch by splitting the crystal into domains, where alternating domains have nonlinear coefficients of opposite signs (Fig. 1b). This technique may be understood using a phasor diagram (Fig. 1c). The wavevector mismatch causes the phases to accumulate differently, and after a finite propagation distance, they will begin to interfere destructively. With quasi-phase matching, the domain periodicity Λ is chosen such that when the process reaches the destructive interference region, the sign of the phasors are flipped, and the process is allowed to continue to build constructively.

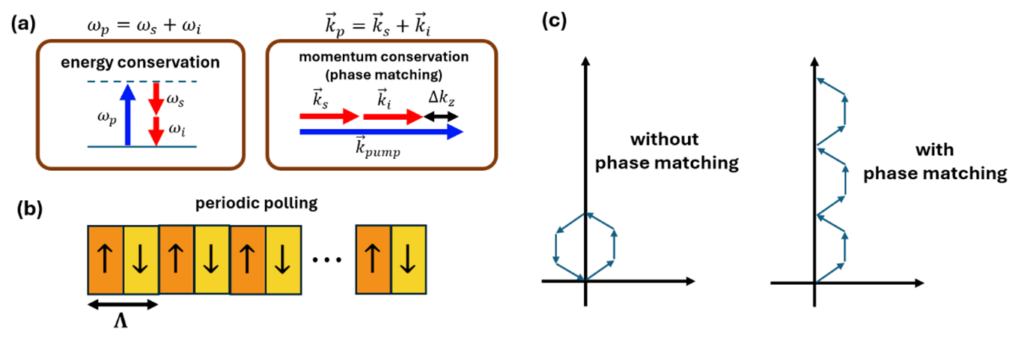
Figure 1. (a) Energy and momentum must be conserved for the SPDC process to be efficient. (b) Periodic poling of the nonlinearity compensates for the wavevector mismatch. (c) Phasor picture of the process accumulation with and without phase matching.

Interestingly, it took until the mid-1980s for this technique to become widespread experimentally [4], using periodic polling. This is because the creation of such domains is challenging, and typically uses ferroelectric domain engineering [5]. This involves the application of a strong electric field to a ferroelectric crystal via patterned electrodes on the crystal surface. This strong field changes the crystal orientation under the electrodes and thus reverses the sign of its nonlinear coefficient. Periodic poling is especially challenging to perform on large-aperture crystals and with small poling periods.

The advantages of quasi-phase matching are that it allows the use of materials with stronger nonlinear coefficients, avoids spatial walk-off, and does not add requirements on the polarization of the different fields. Another advantage is that by tailoring the poling period, different SPDC parameters may be controlled.

For example, as has been shown in [6], using different poling periods could determine whether a type-0 or type-II process will take place. A Type-0 process, where the pump and both generated photons have the same polarization, could be desirable due to its high pair-generation rate. However, it is relatively sensitive to temperature changes and has a large bandwidth. In a type-II process, the two resulting photons have orthogonal polarization, and a narrow spectrum, but the process tends to be weaker.

It is very important to understand the specific application and desired figure of merit before choosing a crystal configuration. For instance, is the total flux the important measure? Or perhaps the total flux per nm of wavelength? Is spatial entanglement a desired feature or something to avoid? Depending on the exact application, a different configuration of pump beam, crystal dimensions, temperature, and poling periodicity may be the best fit [7].

Raicol Crystals is a world-leader in quasi phase matched crystals, and provides periodically poled nonlinear crystals such as PPLN, PPKTP,  and PPSLT, allowing a wide range of periodicities and crystal dimensions. Please contact us for further details! We also provide aperiodically poled KTP (APKTP) crystals, which allow even further control of the resulting quantum state. This will be the subject of another post, so stay tuned!

[1] Walborn, S.P., Monken, C.H., Pádua, S. and Ribeiro, P.S., 2010. Spatial correlations in parametric down-conversion. Physics Reports, 495(4-5), pp.87-139.
[2] Boyd, R.W., Gaeta, A.L. and Giese, E., 2008. Nonlinear optics.
[3] Armstrong, J. A., N. Bloembergen, J. Ducuing, and Peter S. Pershan. “Interactions between light waves in a nonlinear dielectric.” Physical review 127, no. 6 (1962): 1918.
[4] R. Paschotta, article on “Quasi-phase Matching” in the RP Photonics Encyclopedia, retrieved 2024-08-21, https://doi.org/10.61835/kj9
[5] Yamada, M., Nada, N., Saitoh, M. and Watanabe, K., 1993. First‐order quasi‐phase matched LiNbO3 waveguide periodically poled by applying an external field for efficient blue second‐harmonic generation. Applied Physics Letters, 62(5), pp.435-436.
[6] Steinlechner, F., Gilaberte, M., Jofre, M., Scheidl, T., Torres, J.P., Pruneri, V. and Ursin, R., 2014. Efficient heralding of polarization-entangled photons from type-0 and type-II spontaneous parametric downconversion in periodically poled KTiOPO 4. JOSA B, 31(9), pp.2068-2076.
[7] Schneeloch, J., Knarr, S.H., Bogorin, D.F., Levangie, M.L., Tison, C.C., Frank, R., Howland, G.A., Fanto, M.L. and Alsing, P.M., 2019. Introduction to the absolute brightness and number statistics in spontaneous parametric down-conversion. Journal of Optics, 21(4), p.043501.

 

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates.

 

Author: Ronen Shekel

One of the most remarkable features of quantum theory is entanglement, where quantum systems show nonlocal correlations between particles or photons that are impossible to explain using classical physics. This can famously be demonstrated, for example, by violating a Bell inequality [1, 2]. While in many cases entanglement between two-level systems (qubits) is discussed, high-dimensional entanglement between multi-level systems provides an even richer structure.

High-dimensional entangled states are attractive because they have a greater information capacity, and also show increased resistance to noise and losses [3]. Additionally, it is relatively straightforward to generate high-dimensional entangled states using spontaneous parametric down-conversion (SPDC), and to shape them using liquid crystal spatial light modulators [4].

In SPDC [5], a strong plane-wave pump beam impinges upon a nonlinear crystal such as PPKTP (Periodic polled KTP). With some probability, related to the crystal’s nonlinear coefficients, a pump photon will be annihilated, and two entangled photons will be created (Fig. 1a). Since energy must be conserved, the frequencies of these two photons must sum to that of the pump photon, and here we will assume the degenerate case, where they have the same frequency (Fig. 1b). Since momentum must be conserved, the wave vectors of the created photons must add up to that of the pump photon, which is pointing in a specific direction, since the pump is a plane wave. Consequently, the two photons will have anti-correlations in their transverse momentum (Fig. 1c). This means that if one photon is emitted with a certain angle, its twin will be emitted in the opposite direction with respect to the pump beam.

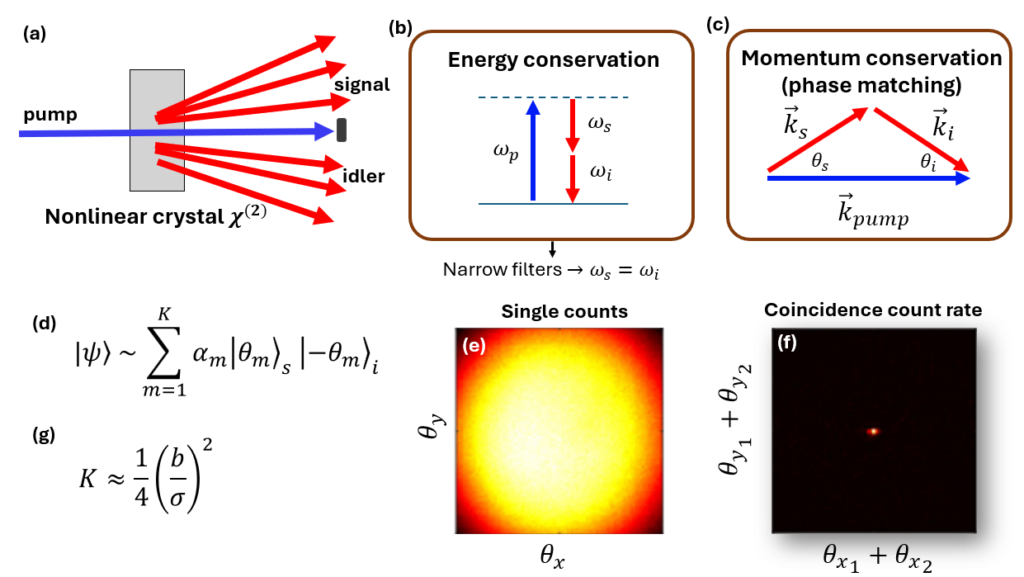
Introduction to spatial entanglement in SPDC and PERIODIC POLLED
Figure 1: (a) Schematic of the SPDC process, which obeys energy (b) and momentum (c) conservation. (d) The resulting quantum state. (e) and (f) are typical single counts and coincidence counts in the far-field of the crystal, for a large Schmidt number. (g) An analytical approximation to the number of modes in the superposition of the state.

In fact, the generated state of these two photons is a coherent superposition of emission in these different angles, each photon in an opposite direction, with coefficients that depend on the exact phase-matching conditions (Fig. 1d), and typically depend on the angles like a sinc function [5]. These correlations may be measured in the far-field. Using a simple camera, we observe the “single counts”, which is the average intensity of photons emitted in all the directions permitted by the phase matching, which may be a rather wide region (Fig. 1e). Performing coincidence measurements, however, will reveal that given that one photon was measured in a certain angle, the twin photon will always be strongly correlated, and will be found in a much smaller “coincidence region” (Fig. 1f).

The ratio between the coincidence region and the single counts region quantifies the number of distinct modes in the quantum superposition, which is related to its Schmidt rank [6, 7] (Fig. 1g). Hence, to tailor the spatial entanglement properties in SPDC, one should consider both the width of the phase matching function (controlling the single counts region) and the strength of the correlations, and plan an optical setup accordingly.

Specifically, the angular width b of the phase matching sinc function, or equivalently, the angular range allowed by the SPDC process, is determined by the pump wavelength λ_p, and by the crystal thickness L, and is approximately. √(λ_p/L) Thus, while using a thin crystal will result in smaller SPDC flux due to a shorter interaction length, it will typically allow a larger range of emission angles, and will generate highly spatially entangled states.

Conversely, the width of the coincidence region is determined by the angular spectrum of the pump, σ. Indeed, for a plane-wave pump with a single well-defined momentum vector, we expect perfect correlations. However, a finite pump beam will necessarily contain many different angles, which will allow an angle mismatch in the momentum conservation. This is referred to more generally as the transfer of angular spectrum from the pump to the SPDC correlations [8].

In conclusion, having a wide pump beam with a narrow angular spectrum, and using a thin crystal, will increase the dimensionality of the SPDC spatial entanglement. The same reasoning about the number of effective modes can equivalently be carried out in the near-field: A wide pump beam yields a correspondingly large emission area of the SPDC photons, and a thin crystal results in each pair of photons being strongly spatially correlated at the output of the crystal due to the small propagation distance traveled from their point of generation [6, 9].

Of course, one doesn’t always want high-dimensional spatial entanglement. For instance, in many cases, SPDC photons are coupled into single-mode fibers. In such a case, we would like to generate only a single spatial mode to get good coupling to the fiber. A good rule of thumb for this is to set the Rayleigh length of the pump to be the length of the crystal.

At Raicol, we provide a variety of nonlinear crystals with a rich range of parameters, allowing you to design your optical setup exactly for your needs. We also provide custom-made periodic polled crystals with specially tailored polling, allowing the shaping of the two-photon joint spectral intensity [10], which will be the subject of a different post. For more information, please visit our products page, and contact us if you have any questions.

[1] Bell, John S. “On the einstein podolsky rosen paradox.” Physics Physique Fizika 1, no. 3 (1964): 195.

[2] Brunner, Nicolas, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. “Bell nonlocality.” Reviews of modern physics 86, no. 2 (2014): 419.

[3] Ecker, Sebastian, Frédéric Bouchard, Lukas Bulla, Florian Brandt, Oskar Kohout, Fabian Steinlechner, Robert Fickler et al. “Overcoming noise in entanglement distribution.” Physical Review X 9, no. 4 (2019): 041042.

[4] Defienne, Hugo, Matthew Reichert, and Jason W. Fleischer. “Adaptive quantum optics with spatially entangled photon pairs.” Physical review letters 121, no. 23 (2018): 233601.

[5] Walborn, Stephen P., C. H. Monken, S. Pádua, and PH Souto Ribeiro. “Spatial correlations in parametric down-conversion.” Physics Reports 495, no. 4-5 (2010): 87-139.

[6] Lib, Ohad. “Utilizing the Spatial Degree of Freedom of Entangled Photons for High-Dimensional Quantum Information Processing”, PhD thesis.

[7] Law, C. K., and J. H. Eberly. “Analysis and interpretation of high transverse entanglement in optical parametric down conversion.” Physical review letters 92, no. 12 (2004): 127903.

[8] Monken, Carlos Henrique, PH Souto Ribeiro, and Sebastiao Pádua. “Transfer of angular spectrum and image formation in spontaneous parametric down-conversion.” Physical Review A 57, no. 4 (1998): 3123.

[9] Schneeloch, James, and John C. Howell. “Introduction to the transverse spatial correlations in spontaneous parametric down-conversion through the biphoton birth zone.” Journal of Optics 18, no. 5 (2016): 053501.

[10] Shukhin, Anatoly, Inbar Hurvitz, Sivan Trajtenberg-Mills, Ady Arie, and Hagai Eisenberg. “Two-dimensional control of a biphoton joint spectrum.” Optics Express 32, no. 6 (2024): 10158-10174.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

 

Author: Ronen Shekel

The Hong-Ou-Mandel (HOM) effect is a cornerstone of modern quantum optics. Originally proposed and demonstrated in 1987 by Chung-Ki Hong, Zhe-Yu Ou, and Leonard Mandel from the University of Rochester [1], the HOM effect considers a simple experiment, where two identical photons enter two ports of a beam splitter. A typical way to generate two such single photons is by using nonlinear crystals, such as PPKTP or BBO.

If one merely measures the number of photons at each output port, both ports will show on average the same counts. However, when measuring coincidence events, where photons arrive at both output ports simultaneously, one finds a quantum interference effect. We notice that there are two possible paths that result with a coincidence event: either both pass the beam splitter, or both are reflected (Fig. 1, left). Since each reflection contributes a factor of   i  to the phase, these two undistinguishable events have opposite phases and interfere destructively, such that no coincidence events will be measured!  

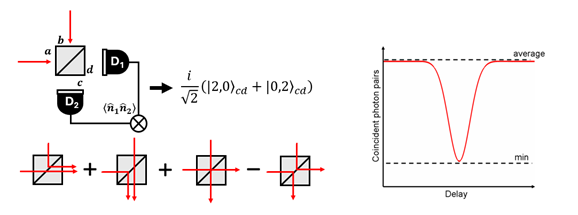
Figure 1 - the Hong-Ou-Mandel effect. When two identical photons enter two ports of a beam-splitter, coincidence events never occur, due to destructive interference (left). The interference visability decreases when delay is introduced between the photons, as they become distinguishable (right).

Note however, that for this interference to occur, the two photons must be completely indistinguishable. If one photon enters the beam splitter a long time after the other (longer than the coherence time of the photons), we will obviously know which photon we are measuring at each detector, and the two states will not interfere destructively. If the photons pass the beam splitter with only a slight delay between them, and their wave packets overlap (photons are not little balls! [2]), the destructive interference will occur, but with lower visibility. This is the origin of the famous “HOM dip” (Fig. 1, right), where  scanning the delay between the two incoming photons results in a dip in the output coincidence counts.

In fact, in the original HOM paper, this effect was suggested as a means to measure sub-picosecond delays between the two photons, and by implication the length of the photon wave packet, with very high accuracy. Since then, the HOM effect has been used in many different contexts [3], and in particular for characterizing single photon sources such as SPDC [4] or quantum dots [5]: the depth of the HOM dip is a measure of the distinguishability between two single photons, while the width of the dip reflects the photons’ coherence length.

Recently, the HOM effect has been utilized in the context of imaging, where the  HOM interference is used to reconstruct the surface depth profile of transparent samples [6]. Identical photons generated using nonlinear crystals and SPDC enter a beam-splitter, where one of the photons first passes through a sample. The different thickness of different areas of the sample induces different delays between the two photons entering the beam-splitter. As discussed above, this will result in a different number of coincidence counts, due to the HOM effect. Thus, the coincidence counts in different pixels of the detectors will reflect the corresponding thickness profile of the sample!

Compared with approaches using classical interference, HOM interference does not require phase stability of the setup, yet it can achieve similar thickness-resolution sensitivity of 1–10 nm.

Other quantum imaging modalities using single and entangled photons, N00N states, or squeezed light provide further advantages, such as sub-shot-noise measurements, better phase sensitivity, and enhanced resolution [7-9].

Besides nonlinear crystals, Raicol is currently developing entangled photon sources, which show excellent HOM visibility, and offer a complete solution for indistinguishable photons. Please contact us for more information!

[1] Hong, Chong-Ki, Zhe-Yu Ou, and Leonard Mandel. “Measurement of subpicosecond time intervals between two photons by interference.” Physical review letters 59.18 (1987): 2044.

[2] Lamb, Willis E. “Anti-photon.” Applied Physics B 60 (1995): 77-84.

[3] Bouchard, Frédéric, Alicia Sit, Yingwen Zhang, Robert Fickler, Filippo M. Miatto, Yuan Yao, Fabio Sciarrino, and Ebrahim Karimi. “Two-photon interference: the Hong–Ou–Mandel effect.” Reports on Progress in Physics 84, no. 1 (2020): 012402.

[4] Kaltenbaek, Rainer, Bibiane Blauensteiner, Marek Żukowski, Markus Aspelmeyer, and Anton Zeilinger. “Experimental interference of independent photons.” Physical review letters 96, no. 24 (2006): 240502.

[5] Sanaka, Kaoru, Alexander Pawlis, Thaddeus D. Ladd, Klaus Lischka, and Yoshihisa Yamamoto. “Indistinguishable photons from independent semiconductor nanostructures.” Physical Review Letters 103, no. 5 (2009): 053601.

[6] Ndagano, Bienvenu, Hugo Defienne, Dominic Branford, Yash D. Shah, Ashley Lyons, Niclas Westerberg, Erik M. Gauger, and Daniele Faccio. “Quantum microscopy based on Hong–Ou–Mandel interference.” Nature Photonics 16, no. 5 (2022): 384-389.

[7] Dowling, Jonathan P., and Kaushik P. Seshadreesan. “Quantum optical technologies for metrology, sensing, and imaging.” Journal of Lightwave Technology 33, no. 12 (2015): 2359-2370.

[8] Moreau, Paul-Antoine, Ermes Toninelli, Thomas Gregory, and Miles J. Padgett. “Imaging with quantum states of light.” Nature Reviews Physics 1, no. 6 (2019): 367-380.

[9] Bowen, W. P., Helen M. Chrzanowski, Dan Oron, Sven Ramelow, Dmitry Tabakaev, Alex Terrasson, and Rob Thew. “Quantum light microscopy.” Contemporary Physics (2023): 1-25.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Ronen Shekel

One of the most beautiful experiments with SPDC light is that of induced coherence. It has originally been demonstrated and analyzed by Zou, Wang, and Mandel in 1991 [1, 2], and is discussed and utilized to this day. In this experiment two nonlinear crystals are used, set in a configuration as shown in Fig. 1.

A “green” pump beam generates via parametric down conversion “yellow” signal and “red” idler photons, both in the first crystal and in the second crystal. We then slightly change the length difference between the paths of the two yellow signal photons and measure their interference using a single photon detector (D1). The question arises – will we measure interference fringes? Are these signals coherent with each other?

induced coherence
Fig 1. The setup of an induced coherence experiment. BS – beam splitter. DM – dichroic mirror. NL – nonlinear crystal. D – single photon detector.

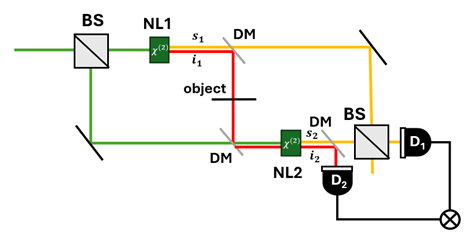
Well, since we cannot know which of the two signal photons we are measuring, we should indeed sum the amplitudes, and do observe interference. However, consider now a case where we block the path of the first idler photon (). Remarkably, even though signal photons can still originate from either the first or the second crystal, the fringes will disappear!

This may again be explained in terms of distinguishability. In Feynman’s words [3]:

If you cannot distinguish the final states even in principle, then the probability amplitudes must be summed.

Further examination of our system shows that blocking the first idler photon does affect the distinguishability between the two signal photons. If the signal photon is accompanied by an idler photon at the second detector (D2) then we know that it originates from the second crystal. If we don’t measure an idler photon – we know that it has been blocked, and that the signal photon originates from the first crystal. Thus, blocking the first idler photon reduces the indistinguishability between the two signal photons.

This is quite remarkable. Even when both processes have a low flux, and statistically, in no point in time the first idler and the second signal photon co-exist, the mere theoretical possibility of measuring the idler photon from the first crystal affects the coherence properties of the signal photon generated in the second crystal. For this reason, we say that the idler photon induces the coherence of the process.

In 2014, this effect has been utilized in the group of Nobel prize winner Anton Zeilinger, in the context of imaging [4]. Consider that we block only part of the path of this idler photon and swap the single photon detector with a sensitive camera. The area on the camera corresponding to the blocked area will show no interference, while the other area will show interference.

Measuring intensity that depends on the transmittance of an object is of course exactly what we want to do in imaging! Notice however the puzzling fact: the light measured by the camera never passed through the object, and the light hitting the object never reaches the camera!

A second modality for using induced coherence for imaging is for phase imaging: the phase accumulated by the idler photon is simply transferred to the signal photon. Such a modality provides interesting configurations such as where the light hitting the object is at a wavelength not detectable by the used camera. Alternatively, it also works when the object is completely transparent or even completely opaque in the wavelength detected by the camera.  

While this imaging technique is no doubt intriguing, providing materials for many new experiments conducted to this day [5], the exact quantum nature of the method has been debated. Indeed, in [6] it has shown that virtually all the features of the experiment can be realized in a quantum-mimetic fashion using classical light. The discussion has since continued, for example in [7] and [8].

In various undetected photon experiments different nonlinear crystals have been used, such as BBO or PPKTP, but in principle almost any nonlinear process could produce similar results [4]. If you want to join the discussion, get your own crystals at Raicol, where we provide the best  world-class  nonlinear crystals and find your own novel imaging modality!

[1]  Zou, X. Y., Lei J. Wang, and Leonard Mandel. “Induced coherence and indistinguishability in optical interference.” Physical review letters 67, no. 3 (1991): 318.

[2] Wang, L. J., X. Y. Zou, and L. Mandel. “Induced coherence without induced emission.” Physical Review A 44, no. 7 (1991): 4614.

[3] Feynman, Richard P. (Richard Phillips), 1918-1988. The Feynman Lectures on Physics. Reading, Mass. :Addison-Wesley Pub. Co., 19631965. Vol. III, chapter 03, “Probability Amplitudes”.

[4] Lemos, Gabriela Barreto, Victoria Borish, Garrett D. Cole, Sven Ramelow, Radek Lapkiewicz, and Anton Zeilinger. “Quantum imaging with undetected photons.” Nature 512, no. 7515 (2014): 409-412.

[5] Pearce, Emma, Osian Wolley, Simon P. Mekhail, Thomas Gregory, Nathan R. Gemmell, Rupert F. Oulton, Alex S. Clark, Chris C. Phillips, and Miles J. Padgett. “Single-frame transmission and phase imaging using off-axis holography with undetected photons.” arXiv preprint arXiv:2403.13389 (2024).

[6] Shapiro, Jeffrey H., Dheera Venkatraman, and Franco NC Wong. “Classical imaging with undetected photons.” Scientific Reports 5, no. 1 (2015): 10329.

[7] Kolobov, Mikhail I., Enno Giese, Samuel Lemieux, Robert Fickler, and Robert W. Boyd. “Controlling induced coherence for quantum imaging.” Journal of Optics 19, no. 5 (2017): 054003.

[8] Lahiri, Mayukh, Armin Hochrainer, Radek Lapkiewicz, Gabriela Barreto Lemos, and Anton Zeilinger. “Nonclassicality of induced coherence without induced emission.” Physical Review A 100, no. 5 (2019): 053839.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

 

Author: Dr. Noa Bloch

Having high threshold damage, LBO crystals for optical parametric amplification (OPA) combined with chirp pulse amplification (CPA)- (OPCPA)  serves as a powerful tool  to achieve very high laser peak powers (Terawatt, Petawatt). How is it done? And why LBO is the most suitable crystal for this task?   

Intense light beams

Ever since lasers were invented 60 years ago, researchers have endeavored to create more intense pulses. There are many implications for intense light pulses in the industry from high precision removal material to ultrafast pulses for surgical procedures and rocket targeting in the military, but strong pulses can also unfold some fundamental questions of the universe. The holy grail of laser physics is a strong laser beam capable of breaking the vacuum of space-time. To this date, we are still a few orders of magnitude away from achieving vacuum decay.  The beam intensity grew extensively over the years, however, by the mid-1980s, scientists stood upon a major challenge around 1 Terawatt of energy density. For short pulses, it was no longer practically possible to increase the intensity of the light without destroying the amplifying material.

Overcoming saturation for increasing pulse energies by chirp pulse amplification (CPA) 

One method for overcoming such energy density limitations would be the increase of the laser amplifier aperture commensurate with the increase of peak power, but the required apertures would be impractically large, laser systems would be highly inefficient as they would not operate near saturation fluence, and would suffer from problems such as transverse parasitic lasing. In December 1985 the physicist Donna Strickland and her supervisor Gérard Mourou had an elegant and simple breakthrough to solve this challenge, inspired by popular science articles on radars. Their invention is simple and easy to describe – take a short laser pulse, stretch it in time, amplify it and squeeze it together again. When a pulse is stretched in time, its peak power is much lower so it can be hugely amplified without damaging the amplifier. The pulse is then compressed in time, which means that more light is packed together within a tiny area of space – and the intensity of the pulse then increases dramatically.

It took a few years for Strickland and Mourou to combine everything successfully but they overcome the technical difficulties. In 1985, Strickland and Mourou were able to prove for the first time that their elegant vision also worked in practice. Their invention, the chirped-pulse amplifier (CPA), increased intense lasers’ energy threshold up to 1 petawatt of energy density.

Combining LBO optical parametric amplifier with CPA – (OPCPA).

A further jump of one order of magnitude came later through a combination of CPA with optical parametric amplifier (OPA), known as OPCPA.  The capability of delivering multi-terawatt power from a staged OPCPA system is due to additional nonlinear crystals.  The most favorite for this task is LiB3O5(LBO), an attractive nonlinear crystal that can support a high efficienct and broadband second and third harmonic generation and high efficient OPCPA. Its recent development for larger size growth makes it possible for high-energy amplification. These factors indicate that a high-peak power laser system can be produced by combining a CPA and LBO booster amplifier. This nearly instantaneous nonlinear process transfers part of the energy from the pump pulse to the seed pulse, creating three outputs: a much stronger seed pulse, or signal pulse; a weakened pump pulse; and a smeared-out idler pulse at the difference frequency between the pump and the seed. A hybrid system with a CPA front end and an OPCPA final amplifier is a potential design for building a compact 10 PW laser. Thanks to LBO crystals, OPCPA has rapidly bridged the gap from its initial modest demonstrations to multi-terawatt and petawatt scale systems in research facilities and universities and numerous lower-power scientific and industrial applications.

Raicols solutins for OPCPA

Recognaising the industry need, Raicol engineered its crystal to deliver the best performance for OPCPA, offering large aperture LBOs. The crystals’ superior surface quality and optical homogeneity contribute to the lowest bulk absorption rates, which is a significant advantage for the nonlinear conversion of high-power lasers. Moreover, the unmatched surface absorption rates of Raicol’s LBO crystals ensure the highest laser damage threshold, making them ideal for high-power laser applications.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

 

Author: Yoad Michael

Photonics plays a significant role in the emerging quantum information industry, and entangled photon pairs are the workhorse of many key applications in quantum optics, where each application utilizes a certain property of the quantum state.

The development of new effective sources of entangled photon pairs (EPS) is crucial for practical applications in the ever-growing field of quantum technologies, spanning from fundamental research in quantum information science, quantum communications, cryptography, sensing, imaging, and more.

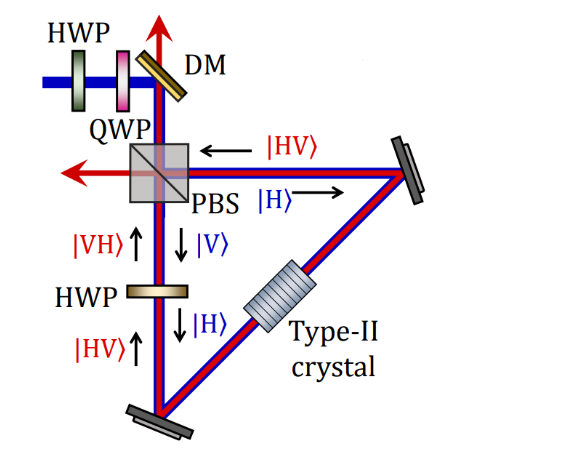
There are several types of entangled photon sources which are based on different quantum states and one important source is based on polarization-entangled photon pairs, which are composed of a superposition of perpendicularly polarized signal and idler.

Unlike squeezed light, which is in principle achieved by a single-pass in a nonlinear gain medium (such as a PPKTP Crystal), polarization-entanglement requires the addition and subtraction of photons, for example by passing through more than one crystal. A recent review paper by the group of Alexander Ling [1] surveys the evolution of sources of polarization-entangled photon pairs throughout the years, as well as their possible applications in quantum communications and cryptography.

Many of the different sources shown in this review paper rely on the PPKTP Crystals that we produce at Raicol – mainly type-0 and type-II phase-matched crystals. However, the sources differ from one another in the way the crystal is utilized.

For example, in a recent quantum cryptography experiment by the University of Science and Technology of China (USTC) [2], a polarization-entangled photon source, based on type-II PPKTP Crystal placed inside a Sagnac interferometer, was used to demonstrate quantum cryptography over a distance of 1,120km. Similarly, a different bell state can also be generated using the same Sagnac configuration, with a type-0 crystal placed instead of the type-II.

Raicol Quantum
Polarization-entanglement from a Sagnac interferometer, adapted from Ref [1].

A different approach for a source of polarization entanglement, utilized by the group of Ling [3], is birefringent splitting and recombination of photon pairs. In this scheme, photon pairs are generated from two spatially-separated pump beams (where one pair experiences polarization rotation), and the beams are recombined using a birefringent material. Compensation crystals are also used to match the temporal delay between the perpendicular pairs.

Birefringent splitting and recombination of beams, adapted from Ref [1].
Birefringent splitting and recombination of beams, adapted from Ref [1].

A third approach, which is currently being explored in Raicol, is the generation of polarization entanglement through domain engineering of the nonlinear crystal, as was shown by Kuo [4]. In this work, the researchers have designed a nonlinear crystal that can perform two simultaneous type-II processes, and showed the polarization-dependent coincidence between the two photons.

Domain-engineered source of orthogonal pairs, adapted from Ref [1].
Domain-engineered source of orthogonal pairs, adapted from Ref [1].

All of these novel methods are part of a general effort to improve sources of polarization-entangled photons, which were initially demonstrated at the intersection of two polarization cones in a type-II BBO Crystal [5]. This process relies on a non-colinear interaction, therefore rendering only a small portion of the down-converted light to be used.

As the world leader in Quasi-phase matching solutions, Raicol Quantum is proud to be part of the next quantum revolution with our advanced periodically polled crystals. For more information: www.raicol-quantum.com

Bibliography

[1] A. Anwar et al. “Entangled photon-pair sources based on three-wave mixing in bulk crystals”, Review of Scientific Instruments 92, 041101 (2021).

[2] J. Yin et al. “Entanglement-based secure quantum cryptography over 1,120 kilometres”, Nature 582, 501-505 (2020).

[3] A. Lohrmann et al. “Broadband pumped polarization entangled photon-pair source in a linear beam displacement interferometer”, Appl. Phys. Lett. 116, 021101 (2020).

[4] P.S Kuo et al. “Demonstration of a polarization-entangled photon-pair source based on phase-modulated PPLN”, OSA Continuum 3, 2, 295-304 (2020).

[5] P.G Kwiat et al. “New High-Intensity Source of Polarization-Entangled Photon Pairs”, Phys. Rev. Lett. 75, 4337 (1995).

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company

Author: Yoad Michael

PPKTP Crystal  is a quasi-phased-matched crystal that converts light of one wavelength into a different wavelength. The original purpose of this crystal was humble: It was designed to be an efficient frequency converter for laser system by second harmonic generation. However, with recent advances in quantum optics, the process of spontaneous parametric down conversion (SPDC) is now the dominating application of PPKTP.

SPDC is a process in which a strong pump beam is converted into correlated photon pairs, coined Signal and Idler. These correlations are the basis for various sources of quantum light, such as heralded single photons, time-energy or polarization entangled photon pairs, and squeezed light.

While it is convenient to consider only the quantum properties these light sources, the nonlinear properties of the interaction play a very significant role. For example, in PPKTP, the phase matching can be fully controlled such that: the signal and idler have the same polarization (type-0) or orthogonal polarization (type-2), same wavelength (degenerate) or separate wavelengths (nondegenerate), emitted along the direction of the pump beam (collinear) or at some angle (noncollinear). The type-0/type-2 is determined by the polling period and is something that needs to be determined at the manufacture stage, while degeneracy and collinearity can be fine-tuned by temperature (to avoid working at bizarre temperatures, it is advised to specify these parameters beforehand and adjust the polling period).

We can dive deeper into these differences. Polarization is not the only optical property that changes between type-0 and type-2 interactions; Spectral bandwidth, pair rate, and tolerance to temperature are also different. This is best illustrated by the wonderful work of the Ursin group [1], in which they compared type-0 and type-2 crystals as sources of polarization entangled photon pairs. As shown in Figure. 1, Type-0 is significantly broader than Type-2 and can be made nondegenerate by temperature tuning. In addition, the authors reported that the pair generation (per nm) of type-0 is about 10 times higher than that of type-2.

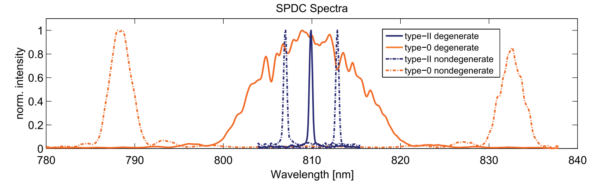
PPKTP Crystal
Figure 1: Comparing the spectral bandwidth and degeneracy of Type-0 and Type-2 ppKTP crystals. Taken from Ref. [1] with permission from the authors.

To make things a little more complicated, the dispersion and the length of the KTP Crystal also affects the spectral bandwidth and pair rate. Longer crystals generate more pairs at the cost of reduced spectral bandwidth, and signal/idler photons are much broader at telecom wavelengths (~1550) than they are at NIR (~810).

All these examples show that PPKTP is an extremely versatile component, and it is therefore important to first consider the needs of each application before choosing the right crystal. Below we present a few recent utilizations of PPKTP for various applications and provide our recommended crystal. We are proud to say that all this knowledge came from the brilliant researchers that use our PPKTP Crystals and shared their findings with the scientific community. Feel free to contact us if you think we are missing a key application or research work.

Boson Sampling and quantum interference

In Boson Sampling, quantum light is usually placed at the input of a large interferometer that includes multiple splitting and re-combining of beams. Boson Sampling relies on quantum interference (Hong-Ou-Mandel effect) and therefore benefits from high spectral purity. Special efforts were made by the Fedrizzi group for creating aperiodically polled crystals for high spectral purity at 1550nm [2], and a similar design was implemented by USTC’s photonic quantum supremacy experiment [3]. Recent quantum computing efforts by Xanadu [4] and QuiX [5] utilized PPKTP at the same wavelength region, due to both higher purity at these wavelengths and compatibility with peripheral platforms such as Silicon Nitride. Raicol has developed (through a collaboration with Prof. Ady Arie) a method for the design and manufacture of high spectral purity APKTP Crystals for Boson sampling and quantum interference close to the group velocity matching point of 1550nm.

Recommended Crystal: Type-2 APKTP or PPKTP at 775->1550. APKTP offers higher spectral purity while PPKTP offers higher pair rate.

Quantum Key Distribution

PPKTP plays a role in entanglement-based QKD as a source of polarization-entangled photon pairs. In this field there are many available options depending on whether the system is designed for free-space or fiber. In general, detector efficiency and the availability of 405nm lasers usually pushes these applications towards entanglement at 810nm [6, 7]. Type-2 crystals are easier to use because of their narrow linewidth, easy separation of the signal and idler with a polarizing beam splitter, and robustness to temperature, while type-0 crystals are broader and offer higher pair rate, making them good candidates for multiplexed QKD [8].

Recommended Crystal: Type-0 or Type-2 PPKTP at 405->810. Type-0 offers higher pair rate and spectral bandwidth, while Type-2 offers ease of usability.

Squeezed Light

Squeezed light usually utilizes the crystals in the strong pumping regime (unlike heralded single photons or polarization entanglement), and benefits from a strong nonlinear response, therefore making type-0 crystals the favorable option. Examples include the Furusawa group with 9dB of squeezing at 860nm [9], The Schnabel group has demonstrated 15dB and 13dB of squeezing at both 1064 and 1550nm [10, 11], and the Bowen group using the former for a demonstration of squeezing-enhanced microscopy [12]. Squeezed light can be generated anywhere from 780nm (390nm pump) to 3.8 microns and is a function of the exact specific application.

When choosing a crystal for squeezed light applications, the researcher should first decide if the squeezing is going to be generated in single-pass or in a cavity. For the former, a standard crystal suffices, while for an optimal parametric oscillator, monolithic or hemi-monolithic options are preferred [13].

Recommended Crystal: Type-0 ppKTP, optional hemi or fully monolithic.

Imaging With Undetected Photons

Imaging with undetected photons usually utilizes type-0 crystals with varying degeneracy. For fundamental research it is convenient to be able to detect both photons [14], while the Ramelow group generated a signal in the visible and idler at the mid-IR for microscopy applications [15].

Recommended Crystal: Type-0 PPKTP, with a period that is designed for nondegeneracy. No better example than Ramelow’s 660->800+3800.

We will try to update this list periodically, so visit this page every now and then!

 

Bibliography

[1] Steinlechner et al. “Efficient heralding of polarization-entangled photons from type-0 and type-II spontaneous parametric downconversion in periodically poled KTiOPO4”, JOSA B 31, 9, 2068-2076 (2014).

[2] Graffitti et al. “Independent high-purity photons created in domain-engineered crystals”, Optica 5, 5, 514-517 (2018).

[3] Zhong et al. “Quantum computational advantage using photons”, Science 370, 6523, 1460-1463 (2020).

[4] Madsen et al. “Quantum computational advantage with a programmable photonic processor”, Nature 606, 75–81 (2022).

[5] Taballione et al. “20-Mode Universal Quantum Photonic Processor”, arXiv:2203.01801.

[6] Yin et al. “Entanglement-based secure quantum cryptography over 1,120 kilometres”, Nature 582, 501–505 (2020).

[7] Mishra et al. “BBM92 quantum key distribution over a free space dusty channel of 200 meters”, Journal of Optics, 24, 7 (2022).

[8] Brambila et al. “Ultrabright Polarization-Entangled Photon Pair Source for Frequency-Multiplexed Quantum Communication in Free-Space”, arXiv:2205.10214.

[9] Takeno et al. “Observation of -9 dB quadrature squeezing with improvement of phase stability in homodyne measurement”, Optics Express 15, 7, 4321-4327 (2007).

[10] Vahlbruch et al. “Detection of 15 dB Squeezed States of Light and their Application for the Absolute Calibration of Photoelectric Quantum Efficiency”, Physical Review Letters 117, 110801 (2016).

[11] Schönbeck et al. “13 dB squeezed vacuum states at 1550 nm from 12 mW external pump power at 775 nm”, Optics Letters 43, 1, 110-113 (2018).

[12] Casacio et al. “Quantum-enhanced nonlinear microscopy”, Nature 594, 201–206 (2021).

[13] Ast et al. “High-bandwidth squeezed light at 1550 nm from a compact monolithic PPKTP cavity”, Optics Express 21, 11, 13572-13579 (2013).

[14] Gilaberte Basset et al. “Video-Rate Imaging with Undetected Photons”, Laser & Photonics Reviews 15, 6 (2021).

[15] Kviatkovsky et al. “Microscopy with undetected photons in the mid-infrared”, Science Advances 6, 42 (2020).

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

Author: Dr. Noa Bloch

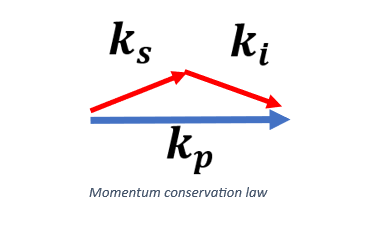
In nonlinear crystals, a special nonlinear process occurs. A pump photon is spontaneously converted into two complementary photons with lower energy. In this process both energy and momentum are conserved, i.e.   and .

In PPKTP Crystal or APKTP Crystal the  momentum mismatch of the process is compensated by the crystal reciprocal vector which is determined by the spatial frequency .

Vacuum energy and momentum fluctuations give rise to the spontaneous creation and annihilation of many random photons.

But the output photons of the SPDC (spontaneous parametric down-conversion nonlinear process) are the ones that conserve momentum and energy.

In type 1 SPDC  all the photon pairs which conserve momentum are positioned on a ring shaped structure:

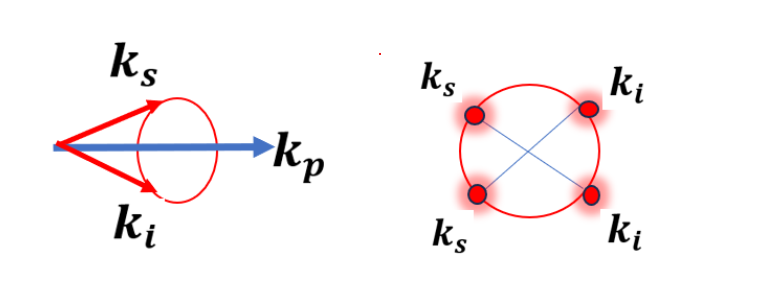
In type 1 SPDC  all the photon pairs which conserve momentum are positioned on a ring shaped structure:

See a movie

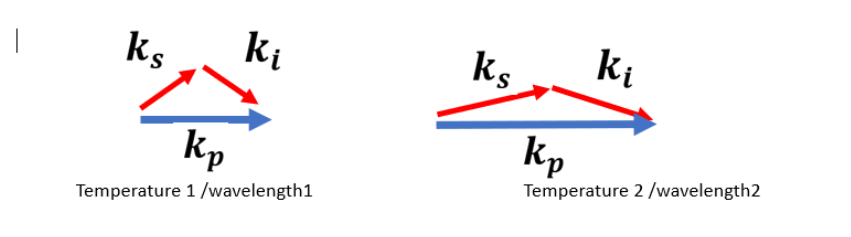
Changing the temperature or wavelength of the crystal will change the phase matching condition thus radius of the rings will be changed as well as seen in the movie.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company

 

A growing number of companies are switching to industrial RTP crystals for electro-optic Pockels cells

In the past year, there has been a growing trend for industrial companies to switch their traditional Pockels cell (PC) components, mostly KD*P, to industrial RTP Crystal.

The excellent EO properties of RTP, its simple setup and configuration, along with its attractive pricing, makes it a great alternative for current PC solutions. Industrial RTP enables increased ROI for a project, by saving time and money for the laser production line and across the product’s lifetime.

 

About RTP

RTP belongs to the KTP Crystal family. The outstanding electro-optical properties of RTP, together with its high damage threshold, enable its use in high-end laser applications, it is ideal for use in applications that require advanced characteristics, such as being non-hygroscopic, having high thermal stability, and for higher-repetition rates.

Raicol’s RTP PC is widely recognized for the following features:

  • Higher laser damage threshold
  • Non-hygroscopic material
  • Low absorption losses
  • No acoustic ringing (up to at least 200kHz)
  • Stability over a wide temperature range (10ºC –50ºC)

 

While providing many advantages over existing solutions, the advanced properties of RTP came with a price tag that prevented its widespread use for industrial applications.

 

Raicol’s new industrial RTP

Raicol’s new iRTP PC is the first product that brings the advantages of RTP to the EO mass market. The modified iRTP PC version of Raicol’s RTP is especially designed for the needs of the industrial laser market. Raicol’s iRTP PC is a standard off-the-shelf RTP PC that offers high performance EO cells at the price level of standard industry PCs.

 

iRTP vs KD*P Benefits

  • Improved thermal stability – iRTP has thermal stability over a wide range of temperatures, eliminating the need for thermal stabilization, thus eliminating the need for an oven or thermal control systems.
  • Reduce laser initiation time – RTP’s high thermal stability reduces laser stabilization and start up times, as well as the overall system initiation time.
  • Simple alignment – iRTP requires only 1D alignment to reach an optimum extinction ratio, in comparison to KD*P, which requires 3D axis control-significantly complexifying the alignment process.
  • Environmental stability- iRTP is a non-hygroscopic material with a temperature compensation design that allows it to function in non-controlled environments with a variety of temperatures and humidity levels.
  • Mechanical robustness and stability – iRTP’s requirement for only 1D alignment means that the iRTP package and mount has a simple and more mechanically stable design. The working parameters do not change throughout the laser’s lifetime, or during temperature changes, hence, requires little to no calibration over time.
  • Small size – The size and footprint of iRTP is much smaller compared to similar KD*P, due to a reduction in assembly, alignment, and temperature control components.
  • High repetition rate – iRTP supports a repetition rate up to 200 kHz.
  • Standard Pockels cell assembly – iRTP is an off-the-shelf product with standard industry EO cell specifications.
  • High damage threshold – iRTPs high damage threshold enables its use for high power lasers.

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Have you already subscribed to our YouTube channel? Don’t miss out—subscribe now for exclusive content and updates from our company.

According to Global Market Insights the electro-optic systems market was valued at USD 12.6 billion in 2022 and is projected to grow at a CAGR of 5.5% to reach USD 20 billion by 2032. Advanced imaging and sensing technologies are driving this growth, especially in surveillance, healthcare, and telecommunications.

Electro-optic systems use electrical signals to control optical properties and are integral to modern applications such as communications, imaging, and sensing. These systems include a range of devices and technologies, including Lasers, LEDs, Cameras, LIDAR, and more.

One of the most important components of these electro-optic systems is the electro-optic cell (EO). Among the materials used in EO cells, RTP (Rubidium Titanyl Phosphate) crystals stand out. RTP crystals belong to the KTP (Potassium Titanyl Phosphate) family and are used in electro-optic applications because of their unique properties.

In this article, we will explore the critical role of electro-optic systems in modern technology, focusing on RTP (Rubidium Titanyl Phosphate) crystals, their benefits, technical specifications, and their applications.

RTP Crystals: The Core of Advanced EO Cells

Rubidium Titanyl Phosphate (RTP), chemically known as RbTiOPO(_4), is an isomorph of the well-known Potassium Titanyl Phosphate (KTP) crystal. Both RTP and KTP belong to the same crystal family and share similar structural properties, ideal for nonlinear and electro-optic applications.

RTP crystals have several unique properties that make them highly advantageous for electro-optic applications:

  • High Damage Threshold: RTP crystals can withstand high laser power densities, approximately 1.8 times higher than KTP, making them suitable for high-power laser systems.
  • High Resistivity: They offer high electrical resistivity, which is beneficial for maintaining performance stability under varying electrical conditions.
  • Non-Hygroscopic: Unlike some other crystals, such as KDP or Rb KD*P, RTP is non-hygroscopic, meaning it does not absorb moisture from the air. This property contributes to its durability and reliability in various environmental conditions.
  • No Piezoelectric Effect: RTP exhibits negligent piezoelectric effect, which can cause unwanted mechanical vibrations in some applications.
  • Wide Temperature Range: The unique design structure performs well over a broad temperature range, from -50°C to +70°C, providing consistent performance in different environments.
  • Low Half-Wave Voltage: RTP crystals require a lower voltage to achieve half-wave retardation, which is crucial for compact and efficient electro-optic devices.
  • High Repetition Rates: Supports high repetition rates, making them ideal for fast switching and modulation applications.

Due to these properties, RTP crystals are widely used in various electro-optic applications, including Q-Switches, Amplitude and Phase Modulators, Pulse Pickers, and Fast Shutters.

Structure and Design of RTP EO Cells

Raicol’s RTP EO cells are designed using a thermally compensated double-crystal configuration. This involves placing two matched RTP crystals in line with the propagation axis (either X or Y axis), with one crystal rotated by 90 degrees relative to the other.

This configuration helps to balance thermal effects, ensuring stable performance across a wide temperature range.

Crystal Orientation and Its Benefits

The specific orientation of the crystals in this configuration offers several benefits:

  • Thermal Compensation: By rotating one crystal by 90 degrees, the thermal expansion effects in one crystal are counteracted by the other, minimizing thermal drift and maintaining consistent performance.
  • Improved Stability: This orientation ensures that the electro-optic properties remain stable over a wide temperature range, from -50°C to +70°C.
  • Improved Homogeneity: The matched pair configuration enhances the homogeneity of the electro-optic effect, allowing for larger cell sizes and more uniform performance.
  • Reduced Piezoelectric Effect: RTP has no ringing effect up to 1MHz and can be used with rep rates way above 1MHz
  • High Repetition Rates: The configuration supports high repetition rates, making it suitable for applications requiring fast switching and modulation.

These design features make Raicol’s RTP EO cells highly reliable and efficient for advanced electro-optic applications, ensuring optimal performance in various demanding environments.

Advantages of Raicol's RTP EO Cells

Raicol’s RTP (Rubidium Titanyl Phosphate) EO (Electro-Optic) cells offer several significant advantages for advanced electro-optic applications:

  • Fast Operation: These cells provide sub-nanosecond response times, providing rapid operation for high-speed applications.
  • Wide Temperature Stability Range: RTP EO cells are designed to operate effectively over a wide temperature range, from -50°C to +70°C, providing reliable performance.
  • High Laser-Induced Damage Threshold: They can withstand high laser power densities, with a damage threshold of up to 1 GW/cm² at 1064 nm, making them ideal for high-power laser systems.
  • Minimal Ringing: The cells exhibit minimal ringing, which is crucial for maintaining high repetition rates, compatible with over 1 MHz repetition rate.
  • Low Half-Wave Voltage: RTP EO cells’ low half-wave voltage allows for a compact design, making them suitable for integration into smaller devices.
  • Non-Hygroscopic Nature: RTP crystals are non-hygroscopic, meaning they do not absorb moisture from the air. This property simplifies handling and storage, as no special covers are needed.
  • Superior Performance in the 400-3000 nm Spectral Range: RTP EO cells perform exceptionally well across a broad spectral range, making them versatile for various optical applications.
  • Low Absorption Losses at 1064 nm: They have very low absorption losses at the common laser wavelength of 1064 nm, leading to efficient operation.
  • High Homogeneity: RTP crystals offer high homogeneity, allowing for the production of large cell sizes, up to 15 x 15 mm² as a standard size.

These advantages make Raicol’s RTP EO cells a preferred choice for applications requiring high performance, reliability, and efficiency.

Applications of RTP EO Cells

RTP (Rubidium Titanyl Phosphate) EO cells are flexible components used in various advanced electro-optic applications due to their unique properties.

Here are some key applications:

Q-Switches and Pulse Pickers

RTP EO cells are used in active Q-switches to control the timing of laser pulses, enabling the generation of high-intensity, short-duration laser pulses. They are also used in pulse pickers to select specific pulses from a train of laser pulses, which is essential for applications requiring precise pulse control.

Phase and Amplitude Modulators

RTP EO cells can modulate the phase of a laser beam, which is crucial for applications like laser stabilization, mode-locking and coherent beam combining (CBC). These cells also control the intensity of laser beams, making them suitable for applications in optical communication and signal processing.

 

Cavity Dumpers and Shutters

RTP EO cells are used in cavity dumpers to rapidly extract energy from a laser cavity, allowing for the generation of high-energy pulses. They act as fast shutters to quickly block or unblock laser beams, which is important for applications requiring precise control of laser exposure.

Attenuators and Deflectors

RTP EO cells can lower the intensity of laser beams, providing adjustable control over the laser power. They also deflect laser beams, enabling precise beam direction and alignment in various optical systems.

Integrated Quantum Photonics and Quantum Computing [ 2 ]

Some other emerging trends in photonics include integrated quantum photonics and quantum computing, which make use of EO technologies for improved information processing and quantum functionality.

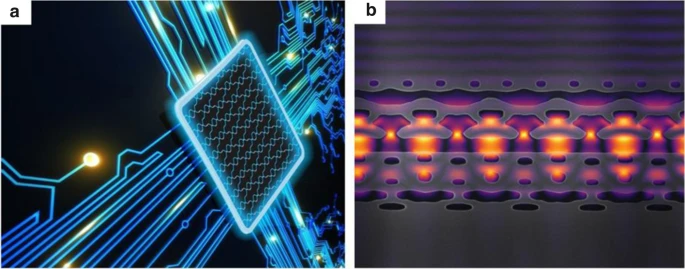
Photonic Integrated Circuits [1]:

Similar to other EO materials RTP can be in a thin film on insulator wafer and enhance performance compared to similar materials. For example, LTOI wafers offer scalable manufacturing at low cost while exhibiting properties similar or superior to lithium niobate-on-insulator (LNOI) wafers. They are used to create high-speed, low-voltage EO modulators and soliton microcombs for high-speed optical communication.

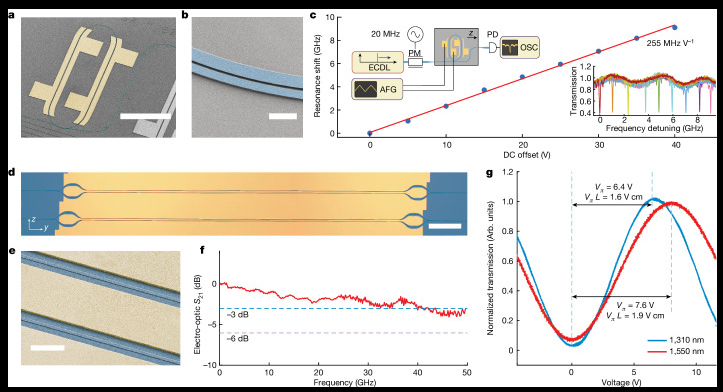
A recent study published in Physics Today [3] discusses the potential of integrating nonlinear optical frequency conversion with EO tunability to improve the performance of integrated photonics. This integration allows for the development of advanced photonic devices that can achieve high-speed data transmission, low power consumption, and enhanced quantum functionality.

Key Findings:

  • Nonlinear Optical Frequency Conversion: This technique involves converting the frequency of light to different wavelengths, which is crucial for applications in telecommunications and quantum computing.
  • EO Tunability: The ability to tune the optical properties of materials using electrical signals improves the flexibility and functionality of photonic devices.

Raicol’s RTP (Rubidium Titanyl Phosphate) crystals can be integrated into these advanced EO systems to enhance their performance. Here’s how professionals can use Raicol’s materials in light of these new developments:

  1. In Silicon Photonics:
  • High-Speed Modulators: RTP crystals can be used to create high-speed modulators with low half-wave voltage, improving the efficiency and compactness of photonic integrated circuits.
  • Increased Data Transmission: The high damage threshold and wide temperature stability range of RTP crystals make them ideal for use in high-power EO modulators, facilitating high-speed data transmission.
  1. In Nonlinear Optical Devices:
  • Frequency Conversion: RTP crystals’ ability to withstand high laser power densities, low absorption losses and high homogeneity makes them suitable for nonlinear optical frequency conversion applications, enhancing the versatility of photonic devices.
  • Quantum Computing: Low absorption losses and high repetition rates of RTP crystals can enhance the reliability and speed of devices used in quantum computing.
  1. In Plasmonic-Organic Hybrid (POH) Devices:
  • Ultrafast Modulation: Improve the performance of POH devices, enabling ultrafast modulation speeds.

Due to these properties, RTP crystals are widely used in various electro-optic applications, including Q-Switches, Amplitude and Phase Modulators, Pulse Pickers, and Fast Shutters.

Technical Specifications

RTP (Rubidium Titanyl Phosphate) EO cells are designed to meet the demanding requirements of various electro-optic applications.

Here are some typical specifications:

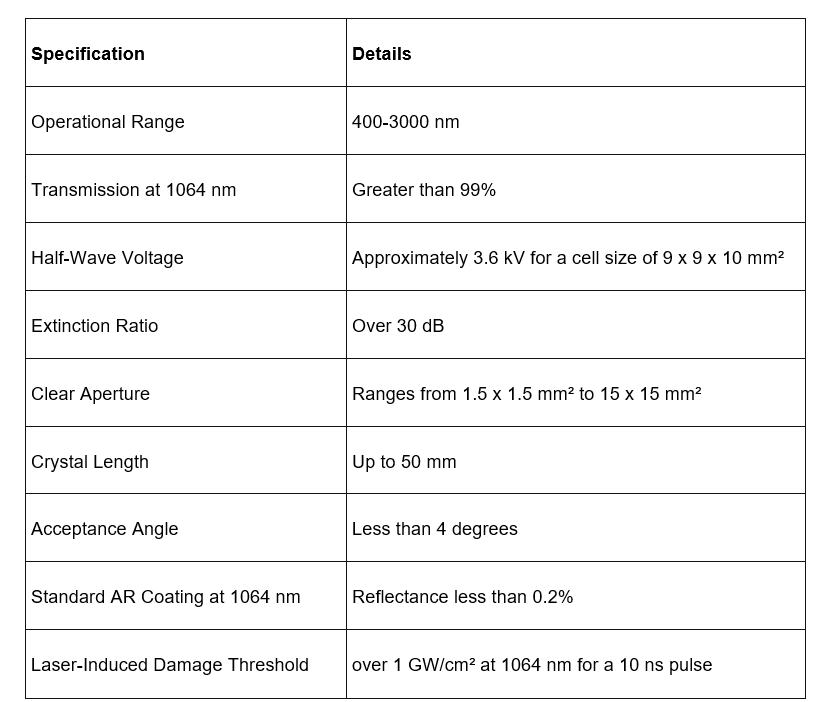
Key Performance Metrics

  • Operational Range: RTP EO cells operate effectively across a broad spectral range of 400-3000 nm, making them versatile for various optical applications.
  • Transmission: They exhibit high transmission rates, with over 99% transmission at the common laser wavelength of 1064 nm, ensuring efficient light passage.
  • Half-Wave Voltage: The low half-wave voltage of around 3.6 kV allows for compact and efficient device designs. Different designs allow to reduce the HWV even more.
  • Extinction Ratio: With an extinction ratio of over 30 dB, RTP EO cells provide excellent modulation depth, which is crucial for high-contrast applications.
  • Clear Aperture: The large clear aperture options, up to 15 x 15 mm², enable the handling of larger beams and higher power levels.
  • Laser-Induced Damage Threshold: The high damage threshold of over 1 GW/cm² at 1064 nm ensures durability and reliability in high-power laser systems1.
  • Temperature Stability: Designed to operate over a wide temperature range from -50°C to +70°C, RTP EO cells maintain stable performance in various environmental conditions.
  • Low Absorption Losses: Very low absorption losses at 1064 nm enhance the efficiency and performance of the EO cells.

Raicol Crystals’ Expertise and Offerings

Raicol Crystals is renowned for its pioneering work in the development and production of high-quality nonlinear optical crystals, including:

  • RTP (Rubidium Titanyl Phosphate): Known for its high damage threshold and excellent electro-optic properties.
  • HGTR KTP (High Gray Track Resistant Potassium Titanyl Phosphate): Offers enhanced resistance to grey tracking, making it suitable for high-power applications.
  • PPKTP (Periodically Poled Potassium Titanyl Phosphate): Widely used in quantum optics and nonlinear frequency conversion applications.

Complete In-House Production Capabilities

Raicol Crystals has a modern manufacturing facility serves as a one-stop shop for high-quality crystal production. Their in-house capabilities include:

  • Crystal Growth: Over 200 crystal growth stations equipped with proprietary growth systems.
  • Optical Fabrication: Advanced cutting, polishing machines, and clean rooms ensure precise and high-quality optical components.
  • Coating Facilities: In-house AR, DBAR, and BBAR coating capabilities for various wavelengths and applications.
  • Testing and Quality Control: Comprehensive testing equipment, including interferometers, spectrophotometers, and laser damage threshold testers, to ensure product reliability and performance.

Flexibility in Production Scale and Fast Delivery Times

Raicol Crystals offers flexibility in production scale, adapting to both mass production and small R&D volumes. Their efficient production processes and extensive experience enable them to provide quick turnaround times to meet customer demands and tailor products to meet specific customer requirements.

These capabilities and offerings make Raicol Crystals a leader in nonlinear optical crystals and electro-optic components, providing reliable and high-performance solutions for various applications.

Conclusion

RTP (Rubidium Titanyl Phosphate) EO (Electro-Optic) cells significantly improve the performance of electro-optic systems by offering superior speed, rates and efficiency. These cells are known for their high damage threshold, ensuring durability and reliability in high-power applications.

Raicol Crystals, a leading provider, offers high-quality RTP EO cells that meet stringent industry and defense standards. Known for innovation and reliability, they serve various industries globally with customized solutions and continuous product improvements through research and development.

References
  1. Wang, C., et al. (2024). Lithium tantalate photonic integrated circuits for volume manufacturing. Nature, 629, 784–790. Access here
  2. Chen, Z., Segev, M. Highlighting photonics: looking into the next decade. eLight 1, 2 (2021). https://doi.org/10.1186/s43593-021-00002-y
  3. 2https://digital.physicstoday.org/physicstoday/august_2023/MobilePagedArticle.action?articleId=1899999#articleId1899999

Do you have a question? Our experts will be happy to hear from you and advise you on the best product for you. Contact Us.

Download Catalog

Skip to content